
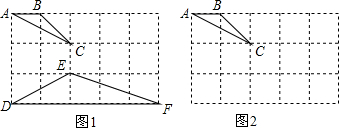
分析 (1)利用勾股定理分别得出三角形各边长,进而利用相似三角形的判定方法得出答案;
(2)利用相似三角形的判定方法,将各边扩大2倍得出答案.
解答 解:(1)△ABC∽△DEF,
理由如下:根据勾股定理可得,
AB=1,BC=$\sqrt{2}$,AC=$\sqrt{5}$,
DE=$\sqrt{5}$,EF=$\sqrt{10}$,DF=5,
∵$\frac{AB}{DE}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,$\frac{BC}{EF}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$,
$\frac{AC}{DF}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$,
∴△ABC∽△DEF;
(2)如图2所示:△A1B1C1即为所求,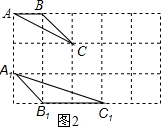 .
.
点评 此题主要考查了相似变换,根据题意得出对应边的长是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | a-πb=9 | B. | xy-y=1 | C. | 5x-y>1 | D. | $\frac{m}{6}+\frac{1}{n}=2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
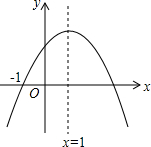 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A. | ac>0 | B. | 当x>1时,y随x的增大而增大 | ||
| C. | 2a+b=1 | D. | 方程ax2+bx+c=0有一个根是x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
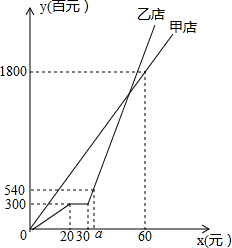 某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:
某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)、(2) | B. | (1)、(3) | C. | (1)、(2)、(3) | D. | (1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com