
分析 (1)利用0指数、负整数指数幂的意义,先乘方,再算加减;
(2)先乘方,再按同底数幂的乘除法法则运算;
(3)利用完全平方公式和平方差公式进行计算;
(4)利用完全平方公式和平方差公式,先算中括号里面的,再做除法.
解答 解:(1)因为($\frac{1}{2}$)-4=16,1.57-π≠0,(1.57-π)0=1
所以原式=-1+16-1
=14.
(2)原式=a2•a4÷a3
=a2+4-3
=a3;
(3)(a+2)2-4(a+1)(a-1)
=a2+4a+4-4(a2-1)
=a2+4a+4-4a2+4
=-3a2+4a+8.
(4)[(4y+3x)(3x-4y)-(y-3x)2]÷4y
=[(3x+4y)(3x-4y)-(y-3x)2]÷4y
=[9x2-16y2-y2+6xy-9x2]÷4y
=(-17y2+6xy)÷4y
=-$\frac{17}{4}$y+$\frac{3}{2}$x.
点评 本题考查了整式的完全平方公式、平方差公式、同底数幂的乘除法、零指数和负整数指数幂的意义.掌握法则和零指数、负整数指数幂的意义是解决本题的关键.注意(-a)n=$\left\{\begin{array}{l}{{a}^{n}(n为偶数)}\\{-{a}^{n}(n为奇数)}\end{array}\right.$


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6 | B. | -$\frac{2}{3}$ | C. | 6 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{1}{2}$ | B. | m<$\frac{1}{2}$ | C. | m≥-$\frac{1}{2}$ | D. | m≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )
如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
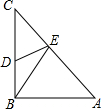 如图,在Rt△ABC中,AB=BC=4,D到为BC的中点,AC边上存在一点E,则△BDE周长的最小值为( )
如图,在Rt△ABC中,AB=BC=4,D到为BC的中点,AC边上存在一点E,则△BDE周长的最小值为( )| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}+2$ | D. | $2\sqrt{3}+2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+2x+1=x(x+2)+1 | B. | (x2-4)x=x3-4x | C. | ax+bx=(a+b)x | D. | m2-2mn+n2=(m-n)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com