
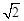 ≈l.414,
≈l.414,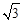 ≈1.732)
≈1.732)
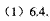
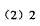
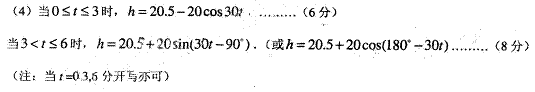

| | 2 |


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源:不详 题型:解答题
 处时的线长为20米,此时小磊正好站在A处,牵引底端
处时的线长为20米,此时小磊正好站在A处,牵引底端 离地面1.5米.假设测得
离地面1.5米.假设测得 ,求此时
,求此时 风筝离地面的大约高度(结果精确到1米,参考数据:
风筝离地面的大约高度(结果精确到1米,参考数据: ,
, ).
).
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.0.6246 | B.0.8121 | C.1.2252 | D.2.1809 |
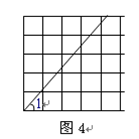
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com