
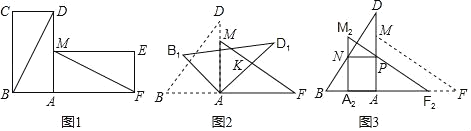
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=4cm,∠ADB=30°.
(1)试探究线段BD与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD与△MEF剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求β的度数.
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
【答案】(1)BD=MF,BD⊥MF;(2)β的度数为60°或15°;(3)平移的距离是(3﹣![]() )cm.
)cm.
【解析】
(1)由旋转的性质得到BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.
(2)分两种情形讨论①当AK=FK时,②当AF=FK时,根据旋转的性质得出结论.
(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出对应线段成比例,即可得到A2A的大小.
(1)结论:BD=MF,BD⊥MF.理由:
如图1,延长FM交BD于点N.
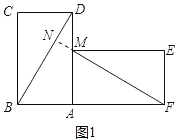
由题意得:△BAD≌△MAF,∴BD=MF,∠ADB=∠AFM.
又∵∠DMN=∠AMF,∴∠ADB+∠DMN=∠AFM+∠AMF=90°,∴∠DNM=90°,∴BD⊥MF.
(2)如图2.

①当AK=FK时,∠KAF=∠F=30°,则∠BAB1=180°﹣∠B1AD1﹣∠KAF=180°﹣90°﹣30°=60°,即β=60°;
②当AF=FK时,∠FAK![]() (180°﹣∠F)=75°,∴∠BAB1=90°﹣∠FAK=15°,即β=15°;
(180°﹣∠F)=75°,∴∠BAB1=90°﹣∠FAK=15°,即β=15°;
综上所述:β的度数为60°或15°;
(3)如图3.
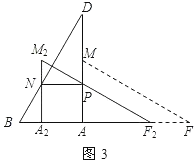
由题意得矩形PNA2A.设A2A=x,则PN=x.在Rt△A2M2F2中,∵F2M2=FM=4,∠F=∠ADB=30°,∴A2M2=2,A2F2=2![]() ,∴AF2=2
,∴AF2=2![]() x.
x.
∵∠PAF2=90°,∠PF2A=30°,∴AP=AF2tan30°=2![]() x,∴PD=AD﹣AP=2
x,∴PD=AD﹣AP=2![]() 2
2![]() x.
x.
∵NP∥AB,∴∠DNP=∠B.
∵∠D=∠D,∴△DPN∽△DAB,∴![]() ,∴
,∴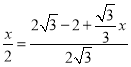 ,解得:x=
,解得:x=![]() ,即A2A=
,即A2A=![]() ,∴平移的距离是(
,∴平移的距离是(![]() )cm.
)cm.


科目:初中数学 来源: 题型:
【题目】已知:如图,AB为![]() 的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
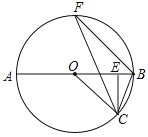
(1)求证:∠OCF=∠ECB;
(2)当AB=10,BC=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上 ,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上 ,称为二次变换,……经过连续2017次变换后,顶点A的坐标是:

A. (4033, ![]() ) B. (4033,0) C. (4036,
) B. (4033,0) C. (4036, ![]() ) D. (4036,0)
) D. (4036,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,5×5正方形方格纸图中,点A,B都在格点处.
(1)请在图中作等腰△ABC,使其底边AC=2![]() ,且点C为格点;
,且点C为格点;
(2)在(1)的条件下,作出平行四边形ABDC,且D为格点,并直接写出平行四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
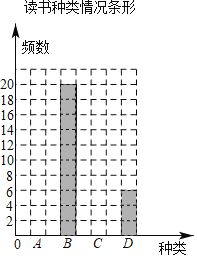
【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=12,弦CD⊥AB于点E,∠DAB=30°,则图中阴影部分的面积是( )

A.18πB.12πC.18π﹣2![]() D.12π﹣9
D.12π﹣9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线交于点O,DF∥AC,CF∥BD.

(1)求证:四边形OCFD是矩形;(2)若AD=5,BD=8,计算tan∠DCF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com