
【题目】如图,菱形ABCD的对角线交于点O,DF∥AC,CF∥BD.

(1)求证:四边形OCFD是矩形;(2)若AD=5,BD=8,计算tan∠DCF的值.
【答案】(1)见解析;(2)tan∠DCF=![]() .
.
【解析】
(1)根据已知条件得到四边形OCFD是平行四边形,根据菱形的性质得到∠DOC=90°,即可得到结论;
(2)根据菱形的性质得到AD=CD,得到CD=5,OD=OB=![]() BD,求得OD=4,根据矩形的性质得到OD=CF,解直角三角形即可得到结论.
BD,求得OD=4,根据矩形的性质得到OD=CF,解直角三角形即可得到结论.
(1)证明:∵DF∥AC,CF∥BD,
∴四边形OCFD是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形OCFD是矩形;
(2)解:∵四边形ABCD是菱形,
∴AD=CD,
∵AD=5,
∴CD=5,
∵菱形ABCD两条对角线交于O,
∴OD=OB=![]() BD,
BD,
∴OD=4,
∵四边形OCFD是矩形,
∴OD=CF,
∴在Rt△CFD中,CF2+DF2=CD2,
∴DF=3,
∴tan∠DCF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
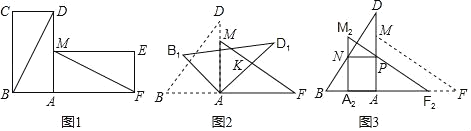
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=4cm,∠ADB=30°.
(1)试探究线段BD与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD与△MEF剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求β的度数.
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴、y轴上,OA=4,OC=3,直线m:y=﹣![]() x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )
x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )

A. 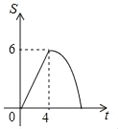 B.
B. 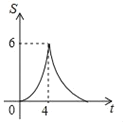 C.
C. 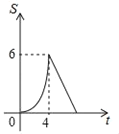 D.
D. 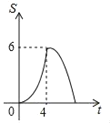
查看答案和解析>>
科目:初中数学 来源: 题型:
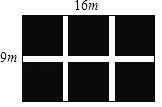
【题目】如图,某小区在一块长为16m,宽为9m的矩形空地上新修三条宽度相同的小路,其中一条和矩形的一边平行,另外两条和矩形的另一边平行,空地剩下的部分种植花草,使得花草区域占地面积为120m2.设小路的宽度为xm,则下列方程:
①(16﹣2x)(9﹣x)=120
②16×9﹣9×2x﹣(16﹣2x)x=120
③16×9﹣9×2x﹣16x+x2=120,
其中正确的是( )
A.①B.②C.①②D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧尚超市准备代销一款运动鞋,每双的成本是160元,为了合理定价,投放市场进行试销.据市场调查,销售单价是200元时,每天的销售量是40双,而销售单价每降低1元,每天就可多售出6双(售价不得低于160元/双),设每双降低售价x元(x为正整数),每天的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每双运动鞋的售价定为多少元时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
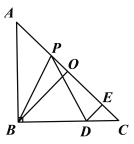
【题目】如图所示,在等腰直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为点E,求证:PE=BO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
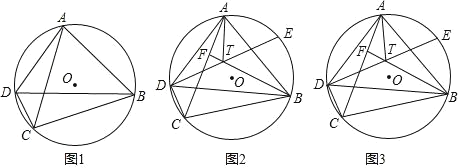
(1)如图1,求证:AC=BC;
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
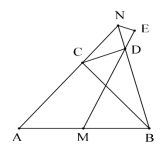
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
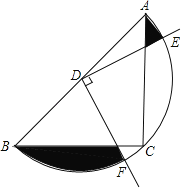
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆,半圆恰好经过△ABC的直角顶点C,以点D为顶点,作∠EDF=90°,与半圆交于点E、F,则图中阴影部分的面积是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com