
【题目】如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( ).
A.a:b:c
B.![]()
C.sinA:sinB:sinC
D.cosA:cosB:cosC
【答案】D
【解析】作出△ABC的外接圆,连接OA、OB、OC,

由垂径定理和圆周角定理可得∠B= ![]() ∠AOC=∠AOE,同理可知∠A=∠BOD、∠C=∠AOF,若设⊙O的半径为R,
∠AOC=∠AOE,同理可知∠A=∠BOD、∠C=∠AOF,若设⊙O的半径为R,
则:OD=Rcos∠BOD=Rcos∠A,
OE=Rcos∠AOE=Rcos∠B,
OF=Rcos∠BOF=Rcos∠C,
故OD:OE:OF=cos∠A:cos∠B:cos∠C.
所以答案是:D.
【考点精析】关于本题考查的垂径定理和圆周角定理,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP的度数是( )
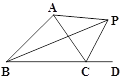
A. 30°; B. 40°; C. 50°; D. 60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【试题背景】已知:l ∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3 , 且d1 =d3 = 1,d2 = 2 .我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.
(1)【探究1】如图1,正方形ABCD为“格线四边形”,BE![]() L于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.
L于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.
(2)【探究2】矩形ABCD为“格线四边形”,其长 :宽 = 2 :1 ,求矩形ABCD的宽
(3)【探究3】如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形, ![]() 于点E, ∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC=DF.
于点E, ∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC=DF.
(4)【拓 展】如图3,l ∥k,等边三角形ABC的顶点A、B分别落在直线l、k上, ![]() 于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE,
于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE, ![]() 于点H.
于点H.
猜想:DH在什么范围内,BC∥DE?直接写出结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图②).

(1)图②中的阴影部分的面积为 ;
(2)观察图②请你写出 (a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)根据(2)中的结论,若![]() ,则(p+q)2= .
,则(p+q)2= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示了 .
(5)试画出一个几何图形,使它的面积能表示(2a+b)(a+2b)=2a2+5ab+2b2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆公共汽车分别自A、B两地同时出发,相向而行。甲车行驶85千米后与乙车相遇,然后继续前进。两车到达对方的出发点等候30分钟立即依原路返回。当甲车行驶65千米后又与乙车相遇,求A、B两地的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的![]() .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 平分
平分![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,请直接写出
,请直接写出![]() 的度数;
的度数;
(3)观察(1)、(2)的结果,猜想![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com