
【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
【答案】
(1)解:根据题意得: ![]() ,
,
解得: ![]()
(2)解:设购买污水处理设备A型设备x台,B型设备(10﹣x)台,根据题意得,
12x+9(10﹣x)≤100,
∴x≤ ![]() ,
,
∵x取非负整数,
∴x=0,1,2,3
∴10﹣x=10,9,8,7
∴有四种购买方案:
①A型设备0台,B型设备10台;
②A型设备1台,B型设备9台;
③A型设备2台,B型设备8台.
④A型设备3台,B型设备7台
(3)解:由题意:220x+180(10﹣x)≥1880,
∴x≥2,
又∵x≤ ![]() ,
,
∴x为2,3.
当x=2时,购买资金为12×2+9×8=96(万元),
当x=3时,购买资金为12×3+9×7=99(万元),
∴为了节约资金,应选购A型设备2台,B型设备8台.
【解析】(1)购买A型的价格是a万元,购买B型的设备b万元,根据购买一台A型号设备比购买一台B型号设备多3万元,购买2台A型设备比购买3台B型号设备少3万元,可列方程组求解.(2)设购买A型号设备x台,则B型为(10﹣x)台,根据使治污公司购买污水处理设备的资金不超过100万元,进而得出不等式;(3)利用每月要求处理污水量不低于1880吨,可列不等式求解.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
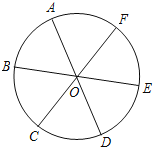
【题目】如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
A.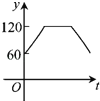 B.
B.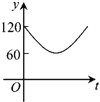 C.
C.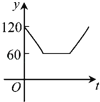 D.
D.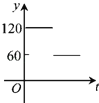
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),其中a,b满足 ![]() +|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
+|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
(1)求点A,B,C的坐标;
(2)点M,N分别为线段BC,OA上的两个动点,点M从点C向左以1.5个单位长度/秒运动,同时点N从点O向点A以2个单位长度/秒运动,如图②所示,设运动时间为t秒(0<t<15).
①当CM<AN时,求t的取值范围;
②是否存在一段时间,使得S四边形MNOB>2S四边形MNAC?若存在,求出t的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= , y= , 并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB=BC=CD=DA,∠A=∠B=∠BCD=∠ADC=90°,点E是AB上一点,点F是AD延长线上一点,且DF=BE.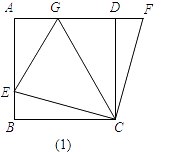
(1)求证:CE=CF;
(2)在图1中,如果点G在AD上,且∠GCE=45°,那么EG=BE+DG是否成立,请说明理由.
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,AD∥BC(BC>AD),∠B=90°,AB=BC=12,点E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com