
【题目】如图1,AB=BC=CD=DA,∠A=∠B=∠BCD=∠ADC=90°,点E是AB上一点,点F是AD延长线上一点,且DF=BE.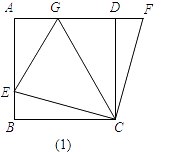
(1)求证:CE=CF;
(2)在图1中,如果点G在AD上,且∠GCE=45°,那么EG=BE+DG是否成立,请说明理由.
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,AD∥BC(BC>AD),∠B=90°,AB=BC=12,点E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
【答案】
(1)
证明:在△CBE和△CDF中,
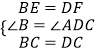 ,
,
∴△CBE≌△CDF,
∴CE=CF;
(2)
解:EG=BE+DG成立,
∵△CBE≌△CDF,
∴CE=CF,∠BCE=∠DCF,BE=DF,
∵∠BCD=90°,∠GCE=45°,
∴∠BCE+∠DCG=45°,
∴∠DCF+∠DCG=45°,即∠FCG=45°,
∴∠FCG=∠GCE,
在△ECG和△FCG中,
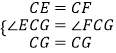 ,
,
∴△ECG≌△FCG,
∴GE=GF,
∴EG=BE+DG;
(3)
作CF⊥AD交AD的延长线于F,
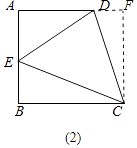
由(2)得,DE=BE+DF,
设DE=x,
∵AB=12,BE=4,
∴AE=8,
∴DF=x﹣4,AD=12﹣(x﹣4)=16﹣x,
由勾股定理得,82+(16﹣x)2=x2,
解得,x=10,
∴DE的长为10.
【解析】(1)证明△CBE≌△CDF,根据全等三角形的性质证明;(2)根据全等三角形的性质得到CE=CF,∠BCE=∠DCF,BE=DF,证明△ECG≌△FCG,根据全等三角形的性质解答;(3)根据(2)的结论和勾股定理计算即可.


科目:初中数学 来源: 题型:
【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题: ![]() =3,
=3, ![]() =0.5,
=0.5, ![]() =6,
=6, ![]() =
= ![]() ,
, ![]() =0.
=0.
根据以上算式,回答:
(1)![]() 一定等于a吗?如果不是,那么
一定等于a吗?如果不是,那么 ![]() =;
=;
(2)利用你总结的规律,计算: ①若x<2,则 ![]() =;
=;
② ![]() = .
= .
(3)若a,b,c为三角形的三边长,化简: ![]() +
+ ![]() +
+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.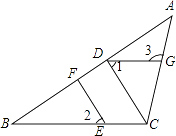
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,试判断DG与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,将△ABC绕点A旋转到△AED的位置,若AE⊥BC,∠ADC=65°,则∠ABC的度数为( )
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校买来钢笔若干枝,可以平均分给(x﹣1)名同学,也可分给(x﹣2)名同学(x为正整数).用代数式表示钢笔的数量不可能的是( )
A.x2+3x+2
B.3(x﹣1)(x﹣2)
C.x2﹣3x+2
D.x3﹣3x2+2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com