
【题目】如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.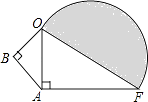
科目:初中数学 来源: 题型:
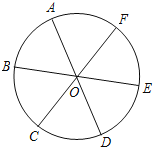
【题目】如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
A.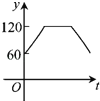 B.
B.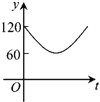 C.
C.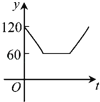 D.
D.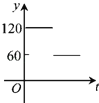
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y=![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y=![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y=![]() 的一个“派生函数”.现给出以下两个命题:
的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=![]() 的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
A. 命题(1)与命题(2)都是真命题
B. 命题(1)与命题(2)都是假命题
C. 命题(1)是假命题,命题(2)是真命题
D. 命题(1)是真命题,命题(2)是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB=BC=CD=DA,∠A=∠B=∠BCD=∠ADC=90°,点E是AB上一点,点F是AD延长线上一点,且DF=BE.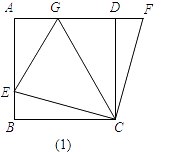
(1)求证:CE=CF;
(2)在图1中,如果点G在AD上,且∠GCE=45°,那么EG=BE+DG是否成立,请说明理由.
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,AD∥BC(BC>AD),∠B=90°,AB=BC=12,点E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com