
 EЈ¬ЙиµгPФЛ¶ЇµДК±јдОЄxЈЁГлЈ©Ј¬ЛД±ЯРОAOCDµДГж»эОЄSЈ®
EЈ¬ЙиµгPФЛ¶ЇµДК±јдОЄxЈЁГлЈ©Ј¬ЛД±ЯРОAOCDµДГж»эОЄSЈ® ЈЁ1Ј©ёщѕЭТ»ґОєЇКэµДЅвОцКЅy=-x+3·Ц±рБоx=0Ј¬Фтy=3Ј»
ЈЁ1Ј©ёщѕЭТ»ґОєЇКэµДЅвОцКЅy=-x+3·Ц±рБоx=0Ј¬Фтy=3Ј» ЎБ3x+
ЎБ3x+ ЎБЈЁ-x2+2x+3Ј©=-
ЎБЈЁ-x2+2x+3Ј©=- x2+
x2+ x+
x+ Ј¬
Ј¬ x2+
x2+ x+
x+ ЈЁ0ЈјxЈј3Ј©Ј¬
ЈЁ0ЈјxЈј3Ј©Ј¬ =
= ·ыєПЈЁ0ЈјxЈј3Ј©Ј¬
·ыєПЈЁ0ЈјxЈј3Ј©Ј¬ =
=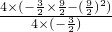 =
=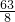 Ј¬
Ј¬ EPЈ¬
EPЈ¬ EPЈ¬
EPЈ¬ ЈЁ-x+3Ј©Ј¬
ЈЁ-x+3Ј©Ј¬ Ј¬x4=3ЈЁІ»єПМвТвЈ¬ЙбИҐЈ©Ј¬
Ј¬x4=3ЈЁІ»єПМвТвЈ¬ЙбИҐЈ©Ј¬ Ј¬0Ј©Ј¬
Ј¬0Ј©Ј¬ Ј¬0Ј©Ј®
Ј¬0Ј©Ј®


| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кЦРЈ¬ЛД±ЯРОOABCКЗµИСьМЭРОЈ¬CBЎОOAЈ¬OA=7Ј¬AB=4Ј¬ЎПCOA=60ЎгЈ¬µгPОЄxЦбЙПµДТ»ёц¶ЇµгЈ¬µ«КЗµгPІ»Улµг0ЎўµгAЦШєПЈ®Б¬ЅУCPЈ¬DµгКЗПЯ¶ОABЙПТ»µгЈ¬Б¬ЅУPDЈ®
ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кЦРЈ¬ЛД±ЯРОOABCКЗµИСьМЭРОЈ¬CBЎОOAЈ¬OA=7Ј¬AB=4Ј¬ЎПCOA=60ЎгЈ¬µгPОЄxЦбЙПµДТ»ёц¶ЇµгЈ¬µ«КЗµгPІ»Улµг0ЎўµгAЦШєПЈ®Б¬ЅУCPЈ¬DµгКЗПЯ¶ОABЙПТ»µгЈ¬Б¬ЅУPDЈ®| BD |
| AB |
| 5 |
| 8 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ЈЁ2012•Уе±±ЗшТ»ДЈЈ©ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кxoyЦРЈ¬ТФЧш±кФµгOОЄФІРДЈ¬3ОЄ°лѕ¶»ФІЈ¬ґУґЛФІДЪЈЁ°ьАЁ±ЯЅзЈ©µДЛщУРХыКэµгЈЁєбЎўЧЭЧш±кѕщОЄХыКэЈ©ЦРИОТвСЎИЎТ»ёцµгЈ¬ЖдєбЎўЧЭЧш±кЦ®єНОЄ0µДёЕВККЗ
ЈЁ2012•Уе±±ЗшТ»ДЈЈ©ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кxoyЦРЈ¬ТФЧш±кФµгOОЄФІРДЈ¬3ОЄ°лѕ¶»ФІЈ¬ґУґЛФІДЪЈЁ°ьАЁ±ЯЅзЈ©µДЛщУРХыКэµгЈЁєбЎўЧЭЧш±кѕщОЄХыКэЈ©ЦРИОТвСЎИЎТ»ёцµгЈ¬ЖдєбЎўЧЭЧш±кЦ®єНОЄ0µДёЕВККЗ| 5 |
| 29 |
| 5 |
| 29 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кЦРЈ¬µИСьМЭРОABCDµДПВµЧФЪxЦбЙПЈ¬ЗТBµгЧш±кОЄЈЁ4Ј¬0Ј©Ј¬DµгЧш±кОЄЈЁ0Ј¬3Ј©Ј¬ФтACі¤ОЄ
ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кЦРЈ¬µИСьМЭРОABCDµДПВµЧФЪxЦбЙПЈ¬ЗТBµгЧш±кОЄЈЁ4Ј¬0Ј©Ј¬DµгЧш±кОЄЈЁ0Ј¬3Ј©Ј¬ФтACі¤ОЄІйїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кxOyЦРЈ¬ТСЦЄµгAЈЁ-5Ј¬0Ј©Ј¬PКЗ·ґ±ИАэєЇКэy=
ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кxOyЦРЈ¬ТСЦЄµгAЈЁ-5Ј¬0Ј©Ј¬PКЗ·ґ±ИАэєЇКэy=| k |
| x |
| k |
| x |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
 ЎПCOA=45ЎгЈ¬¶ЇµгPґУµгOіц·ўЈ¬ФЪМЭРОOABCµД±ЯЙПФЛ¶ЇЈ¬В·ѕ¶ОЄOЎъAЎъBЎъCЈ¬µЅґпµгCК±НЈЦ№Ј®ЧчЦ±ПЯCPЈ®
ЎПCOA=45ЎгЈ¬¶ЇµгPґУµгOіц·ўЈ¬ФЪМЭРОOABCµД±ЯЙПФЛ¶ЇЈ¬В·ѕ¶ОЄOЎъAЎъBЎъCЈ¬µЅґпµгCК±НЈЦ№Ј®ЧчЦ±ПЯCPЈ®Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com