
【题目】如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2 , 则S与t之间的函数关系图象大致为( )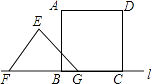
A.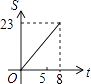
B.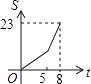
C.
D.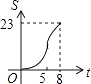
【答案】D
【解析】解:当0≤t≤5时,
设FG与AB交于点H,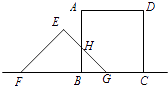
∴正方形与三角形重合部分的面积是△BHG的面积,
∴BG=t,
∵∠EGF=45°,
∴BH=BG=t,
∴S= ![]() BGBH=
BGBH= ![]() t2 ,
t2 ,
当5<t≤8时,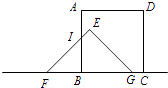
设EF与AB交于点I,
∴正方形与三角形重合部分的面积是四边形BIEG的面积,
∴BG=t,
∴FB=10﹣t,
∵∠EFG=45°,
∴FB=BI=10﹣t,
又∵△EFG的面积为: ![]() =25,
=25,
∴S=25﹣ ![]() FBBI=25﹣
FBBI=25﹣ ![]() (10﹣t)2=﹣
(10﹣t)2=﹣ ![]() t2+10t﹣25,
t2+10t﹣25,
故选(D)
【考点精析】通过灵活运用函数的图象,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
则下列判断正确的是( )
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=4时,y>0
D.方程ax2+bx+c=0的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=1,BC= ![]() ,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC= .
,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC= . 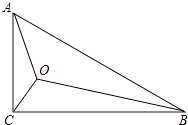
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.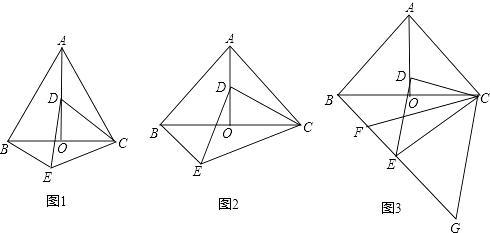
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求 ![]() 的值;
的值;
(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=k2x+b的图象交于点P(m,﹣1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.
的图象与一次函数y=k2x+b的图象交于点P(m,﹣1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ. 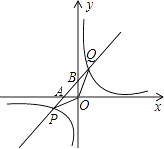
(1)求两函数的解析式;
(2)求证:△POB≌△QOA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1 , 第二次将点A1向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 按照这种移动规律移动下去,第n次移动到点An , 如果点An与原点的距离不小于20,那么n的最小值是 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.
请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+![]() , PA=
, PA=![]() , 则:
, 则:
①线段PB= ,PC= ;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为 ;
(2)如图② , 若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足![]() , 求
, 求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com