
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 和B两点,与x轴交于点C.
和B两点,与x轴交于点C.
(1)求反比例函数的解析式及点C的坐标.
(2)求△OCA的面积

【答案】(1) ![]() ,C(3.0);(2) 3.
,C(3.0);(2) 3.
【解析】
(1)先把点A代入一次函数解析式求出a,再把点A代入反比例函数的解析式即可求出k,即可求出反比例函数解析式;令一次函数y=0,可求出C的坐标.
(2)连接OA,过点A作![]() 于点D, 先算出△OCE和△OAE的面积,所求面积就是△OCE的面积-△OAE的面积,即可求得结果.
于点D, 先算出△OCE和△OAE的面积,所求面积就是△OCE的面积-△OAE的面积,即可求得结果.
(1)由题可知点A既在一次函数图象上,又在反比例函数图象上,把点![]() 代入
代入![]() 中,得
中,得![]() ,
,
∴![]() ,
,
把点A代入![]() 中,得到k=2.
中,得到k=2.
∴反比例函数的解析式为![]() .
.
由图可知,点C是一次函数图象与x轴的交点,令一次函数y=0,可得x=3,
∴![]() .
.
∴反比例函数的解析式为![]() ,C点的坐标为
,C点的坐标为![]() .
.
(2)如图,连接OA,过点A作![]() 于点D,
于点D,
由(1)可得![]() ,
,
∴AD=1,
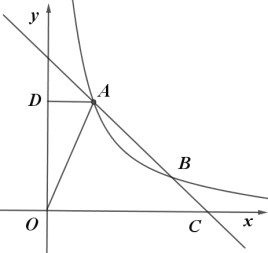
由图可知,E点是一次函数与y轴的交点,
∴![]() ,
,
∴OE=3,
又∵OC=3,
∴![]() ,
,
![]() ,
,
∴![]() .
.
所以△OCA的面积是3.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向上平移3个单位后,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1的坐标.
(2)将△ABC绕点O顺时针旋转90°,请画出旋转后的△A2B2C2,并求点B所经过的路径长(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于E,DF⊥AC于点F.
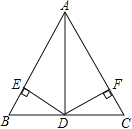
(1)请写出与A点有关的三个正确结论;
(2)DE与DF在数量上有何关系?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)乙车休息了 _________ h;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察数轴,请回答:
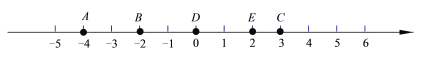
(1)点C与点D的距离为______ ,点B与点D的距离为______ ;
(2)点B与点E的距离为______ ,点A与点C的距离为______ ;
发现:在数轴上,如果点M与点N分别表示数m,n,则他们之间的距离可表示为 ______(用m,n表示)
(3)利用发现的结论解决下列问题: 数轴上表示x的点P与B之间的距离是1,则 x 的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
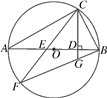
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=12,∠BCD=120°,求四边形AODE的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,已知DE﹦DF,∠EDF=∠A。
(1)找出图中相似的三角形,并证明;
(2)求证: ![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com