
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,已知DE﹦DF,∠EDF=∠A。
(1)找出图中相似的三角形,并证明;
(2)求证: ![]() .
.

【答案】(1)△ABC∽△DEF,证明见解析;(2)证明见解析.
【解析】试题分析:此题的证明方法比较多,可以选择如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似,因为都是等腰三角形,对应边成比例,且夹角相等,所以相似;再利用相似三角形的对应边成比例证得: ![]() .
.
试题解析:(1)△DEF∽△ABC,△BDE∽△CEF.
证明如下:∵AB=AC,DE=DF,
∴![]() .
.
∵∠EDF=∠A,
∴△DEF∽△ABC.
∴∠DEF=∠B=∠C.
∵∠BED+∠DEF+∠FEC=∠C+∠CFE+∠FEC=180°,
∴∠BED=∠CFE.
∴△BDE∽△CEF.
(2)证明:∵△BDE∽△CEF,
∴![]() .
.
∵△DEF∽△ABC,
∴![]() .
.
∴![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 和B两点,与x轴交于点C.
和B两点,与x轴交于点C.
(1)求反比例函数的解析式及点C的坐标.
(2)求△OCA的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类: ![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.

根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,动点E从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.
(1)当t=1.5时,S=________;当t=3时,S=________.
(2)设DE=y1,AG=y2,在如图所示的网格坐标系中,画出y1与y2关于t的函数图象.并求当t为何值时,四边形DEGF是平行四边形?
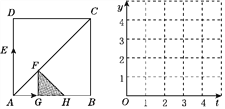
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c在数轴上对应的点如图所示,
![]()
(1)化简:2|b﹣c|﹣|b+c|+|a﹣c|﹣|a﹣b|;
(2)若(c+4)2与|a+c+10|互为相反数,且b=|a﹣c|,求(1)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC在直角坐标系中.
(1)请直接写出点A、C两点的坐标:
(2)三角形ABC的面积是 ;
(3)若把三角形ABC向上平移1个单位,再向右平移1个单位得三角形A′B′C′在图中画出三角形A′B′C’,这时点B′的坐标为 .
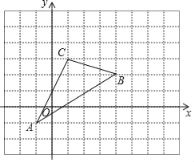
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在RtΔABC中,∠ABC=90°,0为AC的中点.
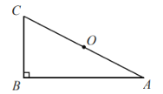
求作:四边形ABCD,使得四边形ABCD为矩形.
作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO;
②连接AD,CD,则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)使用直尺和圆规,在图中补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∴点O为AC的中点,
∴AO=CO.
又∵DO=BO,
∵四边形ABCD为平行四边形(__________)(填推理的依据).
∵∠ABC=90°,
∴![]() ABCD为矩形(_________)(填推理的依据).
ABCD为矩形(_________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递配送员在一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,某天他从出发点开始所行走的路程记录为(单位:千米):
+10、-3、-5、+4、+6、+5、-3、-6、-4、+10
(1) 在送快递过程中最远距出发点___________千米
(2) 这天送完最后一个快递时,在出发点的什么方向,距离出发点是多少千米?
(3) 如果送完快递后,需立即返回出发点,那么他这天送快递(含返回)共耗油多少升(已知每千米耗油0.2升)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com