
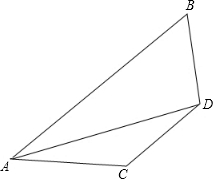
 如图所示,已知AD平分∠BAC,∠ACD+∠B=180°,求证:BD=CD.
如图所示,已知AD平分∠BAC,∠ACD+∠B=180°,求证:BD=CD. 分析 过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,证明△DMB≌△DNC,即可得出结论.
解答 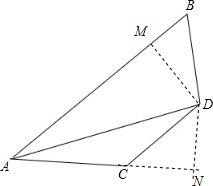 证明:过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,
证明:过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90,
∵∠ACD+∠B=180,∠ACD+∠DCN=180,
∴∠B=∠DCN,
在△BDM与△CDN中,$\left\{\begin{array}{l}{∠B=∠DCN}\\{∠BMD=∠CND}\\{DM=DN}\end{array}\right.$,
∴△DMB≌△DNC (AAS),
∴BD=CD.
点评 本题考查了全等三角形的判定与性质,正确的作出辅助线构造全等三角形是解题的关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
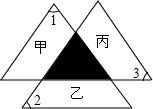 如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )
如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )| A. | 乙>甲>丙 | B. | 乙>丙>甲 | C. | 丙>甲>乙 | D. | 丙>乙>甲 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
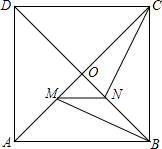 如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.
如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
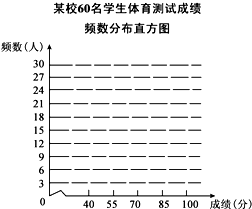 某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表| 成绩 | 划记 | 频数 | 百分比 |
| 优秀 | 正正正 | a | 30% |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 15% |
| 不合格 |  | 3 | 5% |
| 合计 | 60 | 60 | 100% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com