
分析 (1)首先根据题意画出树状图,然后由树状图即可求得所有等可能的结果;再由点Q在y轴上的有:(-2,0),(0,0),(0,1)利用概率公式即可求得点Q在y轴上的概率;
(2)因为当点Q在圆上或在圆外时,过点Q能作⊙O切线,由在⊙O外的有(-2,1),(-2,-2),在⊙O上的有(0,-2),(-2,0),利用概率公式即可求得答案.
解答  解:(1)画树状图得:
解:(1)画树状图得:
则点Q所有可能的坐标有:(-2,0),(0,0),(1,0),(-2,-2),(0,-2),(1,-2);
∵点Q在y轴上的有:(0,-2),(0,0),
∴点Q在y轴上的概率为:$\frac{1}{3}$;
(2)∵⊙O的半径是2,
∴在⊙O外的有(-2,-2),(-2,1)在⊙O上的有(0,-2),(-2,0),
∴过点Q能作⊙O切线的概率为:$\frac{2}{3}$.
点评 此题考查了列表法与树状图法求概率的知识.此题难度适中,注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
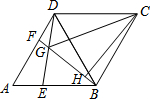 如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.
如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
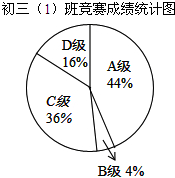 初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )
初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )| A. | B级人数比A级人数少21 | B. | 50人得分的众数是22 | ||
| C. | 50人得分的平均数是80 | D. | 50人得分的中位数是80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
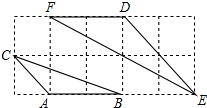 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 度数 | 9 | 10 | 11 |
| 天数 | 3 | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com