练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点．四边形ABCD的顶点在格点上，点E是边DC与网格线的交点．请选择适当的格点，用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．

    （1）如图1，过点A画线段AF，使AF∥DC，且AF=DC．

    （2）如图1，在边AB上画一点G，使∠AGD=∠BGC．

    （3）如图2，过点E画线段EM，使EM∥AB，且EM=AB．

    【答案】（1）作图见解析；（2）作图见解析；（3）作图见解析.

    【解析】

    （1）作平行四边形AFCD即可得到结论；

    （2）根据等腰三角形的性质和对顶角的性质即可得到结论；

    （3）作平行四边形AEMB即可得到结论．

    （1）如图所示，线段AF即为所求；

    （2）如图所示，点G即为所求；

    （3）如图所示，线段EM即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学以致用：问题1：怎样用长为的铁丝围成一个面积最大的矩形？

    小学时我们就知道结论：围成正方形时面积最大，即围成边长为的正方形时面积最大为．请用你所学的二次函数的知识解释原因．

    思考验证：问题2：怎样用铁丝围一个面积为且周长最小的矩形？

    小明猜测：围成正方形时周长最小．

    为了说明其中的道理，小明翻阅书籍，找到下面的结论：

    在、均为正实数）中，若为定值，则，只有当时，有最小值．

    思考验证：证明：、均为正实数）

    请完成小明的证明过程：

    证明：对于任意正实数、

    　　

    解决问题：

    （1）若，则　　（当且仅当　　时取“” ；

    （2）运用上述结论证明小明对问题2的猜测；

    （3）填空：当时，的最小值为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图像如图所示．

    （1）当时，说明这个二次函数的图像与x轴必有两个交点；

    （2）如图情况下，若，求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米.设这个苗圃园垂直于墙的一边的长为x米

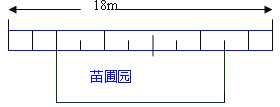
    （1）用含x的代数式表示平行于墙的一边的长为＿＿＿＿米，.x的取值范围为＿＿＿＿

    （2）这个苗圃园的面积为88平方米时，求x的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠C=90°，点P为AC边上的一点，延长BP至点D，使得AD=AP，当AD⊥AB时，过D作DE⊥AC于E，AB-BC=4，AC=8，则△ABP面积为_____

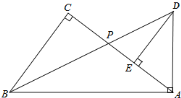
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ACB和△DCE均为等腰三角形，点A、D、E在同一条直线上，BC和AE相交于点O，连接BE，若∠CAB=∠CBA=∠CDE=∠CED=50°。

    （1）求证：AD=BE；

    （2）求∠AEB。　　

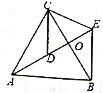
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，已知点A（8，0）和点B（0，6），点C是AB的中点，点P在折线AOB上，直线CP截△AOB，所得的三角形与△AOB相似，那么点P的坐标是_____．

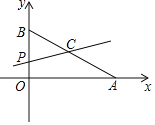
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC为等腰直角三角形，∠ACB=90°，抛物线经过A，B两点，其中点A，C的坐标分别为（1，0），（﹣4，0），抛物线的顶点为点D．

    （1）求抛物线的解析式；

    （2）点E是直角三角形ABC斜边AB上的一个动点（不与A，B重合），过点E作x轴的垂线，交抛物线于点F，当线段FE的长度最大时，求点E的坐标；

    （3）在（2）的条件下，抛物线上是否存在一点P，使△PEF是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

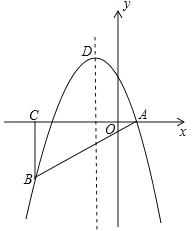
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=4，BC=6，E是BC边的中点，点P在线段AD上，过P作PF⊥AE于F，设PA=x．

    （1）求证：△PFA∽△ABE；

    （2）当点P在线段AD上运动时，设PA=x，是否存在实数x，使得以点P，F，E为顶点的三角形也与△ABE相似？若存在，请求出x的值；若不存在，请说明理由；

    （3）探究：当以D为圆心，DP为半径的⊙D与线段AE只有一个公共点时，请直接写出x满足的条件：　 　．

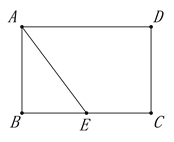
    备用图

    查看答案和解析>>

    同步练习册答案