
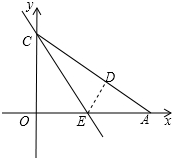
 如图,在平面直角坐标系xOy中,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于点A、C,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
如图,在平面直角坐标系xOy中,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于点A、C,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.分析 (1)根据∠CAO=30°,由折叠可知∠OCE=∠ECD=$\frac{1}{2}$∠OCA=30°,在Rt△COE中,利用三角函数可求OE的值,从而可求点E的坐标是(1,0),然后求出点C的坐标,设直线CE的解析式为y=kx+b,将C、E的坐标代入,可得到关于k、b的方程组,解之即可;
(2)在Rt△AOC中,利用三角函数可求出AC、AO的值,继而求出AD的值,过点D作DF⊥OA于点F,在Rt△AFD中,利用三角函数可求DF、AF的值,然后根据OF=AO-AF求出OF的值,从而求得点D的坐标;
(3)需分情况讨论:
第一种情况:若此点在第四象限内,可设其为M1,延长DF交直线CE于M1,连接M1O,则有DM1∥y轴,求出点M1的坐标;
第二种情况:此点在第二象限内,设为M2.可过点D作DN∥CE交y轴于N,过N点作NM2∥CD交直线CE于点M2,则四边形M2NDC为平行四边形,求出点M2的坐标即可.
解答 解:(1)由题意知∠CAO=30°,
∴∠OCE=∠ECD=$\frac{1}{2}$∠OCA=30°,
∵直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于点A、C,
∴C(0,$\sqrt{3}$),
∴在Rt△COE中,OE=OC•tan∠OCE=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,
∴点E的坐标是(1,0),
设直线CE的解析式为y=kx+b.
把点C(0,$\sqrt{3}$),E(1,0)代入得$\left\{\begin{array}{l}{b=\sqrt{3}}\\{k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=\sqrt{3}}\end{array}\right.$.
∴直线CE的解析式为y=-$\sqrt{3}$x+$\sqrt{3}$;
(2)在Rt△AOC中,AC=$\frac{OC}{sin∠CAO}$=2$\sqrt{3}$,
AO=$\frac{OC}{tan∠CAO}$=3,
∵CD=OC=$\sqrt{3}$,
∴AD=AC-CD=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$,
过点D作DF⊥OA于点F,
在Rt△AFD中,DF=AD•sin∠CAO=$\frac{\sqrt{3}}{2}$,
AF=AD•cos∠CAO=$\frac{3}{2}$,
∴OF=AO-AF=$\frac{3}{2}$,.
∴点D的坐标是($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
(3)存在两个符合条件的M点,第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1,
连接M1O,M1O∥AC,
则有DM1∥y轴,
∵OF=$\frac{3}{2}$,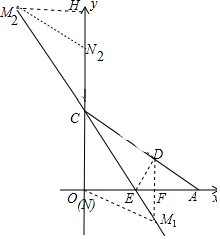
∴设点M1的坐标为($\frac{3}{2}$,y1),
又∵点M1在直线CE上,
∴将点M1的坐标代入y=-$\sqrt{3}$x+$\sqrt{3}$中,
得y1=-$\sqrt{3}$×$\frac{3}{2}$+$\sqrt{3}$=-$\frac{\sqrt{3}}{2}$,即FM1=$\frac{\sqrt{3}}{2}$.
∴点M1的坐标是($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$),
又∵DM1=DF+FM1=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,OC=$\sqrt{3}$,
∴DM1=OC,
又∵DM1∥OC,
∴四边形CDM1O为平行四边形,
又∵点O在y轴上,
∴点M1是符合条件的点.
第二种情况:此点在第二象限内,设为M2,
过点D作DN∥CE交y轴于N,过N点作NM2∥CD交直线CE于点M2,
则四边形M2N2DC为平行四边形,
∴M2N=CD=$\sqrt{3}$,
∵M2N∥CD,DN∥CE,
∴∠NM2C=∠ACE,∠OCE=∠M2CN,
∴CN=M2N,
∵M2N=CD=$\sqrt{3}$,
∴CN=$\sqrt{3}$,
作M2H⊥y轴于点H,
∵M2N∥CD,
∴∠M2NC=∠NCD,
∴∠M2NH=∠OCA=60°,
在Rt△M2NH中,
M2H=M2N•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
NH=M2N•cos60°=$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,
∴HO=HN+CN+OC=$\frac{5\sqrt{3}}{2}$,
∴M2(-$\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$),
∴点M2是符合条件的点,
综上所述,符合条件的两个点的坐标分别为M1($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$),M2(-$\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$).
点评 本题考查了一次函数的综合应用,涉及了一元二次方程的根,待定系数法求函数的解析式、勾股定理、全等三角形的性质等知识点的应用,解决这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6.7×105米 | B. | 6.7×106米 | C. | 6.7×107米 | D. | 6.7×108米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
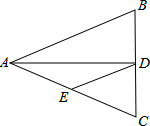 如图,△ABC中,AB=AC=12,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长是( )
如图,△ABC中,AB=AC=12,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长是( )| A. | 20 | B. | 12 | C. | 16 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
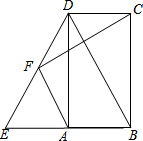 如图,在矩形ABCD中,E在BA延长线上,连接DE,F在DE上,连接AF、FC,且BE=BD.
如图,在矩形ABCD中,E在BA延长线上,连接DE,F在DE上,连接AF、FC,且BE=BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com