
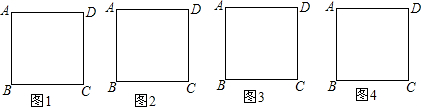
���� ��1���ɰ������ηָ�Ϊ�ĸ�ȫ�ȵ������Σ�������Щ�����εĶԽ��ߣ���װ�÷��ڽ��㴦�����㵽�������С�����ζ���ľ������ͨ�����㿴�Ƿ��ʺϣ�
��2���ɣ�1���õ���ʾ���������ηָ�Ϊ���������Σ���ߵ�һ�����εĶԽ����ܷ�������ֱ��Ϊ31�����ܷ������װ�÷������������εĶԽ��ߵĽ��㴦��
��� 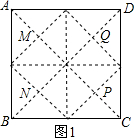 �⣺��1����ͼ1���������εȷֳ���ͼ���ĸ�С�����Σ�����4��ת��װ�ð�װ����4��С�����ζԽ��ߵĽ��㴦��
�⣺��1����ͼ1���������εȷֳ���ͼ���ĸ�С�����Σ�����4��ת��װ�ð�װ����4��С�����ζԽ��ߵĽ��㴦��
��ʱ��ÿ��С�����εĶԽ��߳�Ϊ$\frac{1}{2}$��30$\sqrt{2}$=15$\sqrt{2}$��31��ÿ��ת��װ�ö�����ȫ����һ��С����������
�ʰ�װ4������װ�ÿ��ԴﵽԤ���Ҫ��
��2�����ԣ��������£�
��ԭ�����ηָ����ͼ2�е�3�����Σ�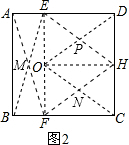 ʹ��BE=31��H��CD���е㣨��OD=OC����
ʹ��BE=31��H��CD���е㣨��OD=OC����
��ÿ��װ�ð�װ����Щ���εĶԽ��߽��㴦��
��AE=$\sqrt{3{1}^{2}-3{0}^{2}}$��DE=30-$\sqrt{61}$��
��OD=$\sqrt{��30-\sqrt{61}��^{2}+1{5}^{2}}$��26.8��31��
����˰�װ�������ת��װ�ã�Ҳ�ܴﵽԤ��Ҫ��
���� ����Ӧ���������ͼ���������Ĺؼ��������ó���ͼ�εõ����ʵļ��㷽����˼·��Ȼ�������ȷ������ø��ǵ�������õ������ƵĽ⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3•a2=a6 | B�� | ��a3��2=a6 | C�� | a3+a2=a6 | D�� | a3-a2=a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ac��bc | B�� | $\frac{1}{a}$$��\frac{1}{b}$ | C�� | |a|��|b| | D�� | ac2��bc2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
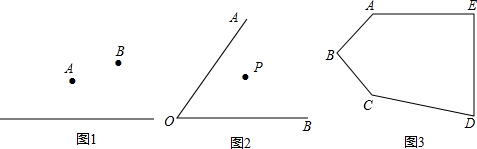
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com