
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() ,其中
,其中![]() .
.
(1)求证:此方程有两个不相等的实数根;
(2)若等腰![]() 的一腰
的一腰![]() 长为6,另两边
长为6,另两边![]() ,
,![]() 的长分别是这两个方程两个不相等的实数根,求等腰
的长分别是这两个方程两个不相等的实数根,求等腰![]() 的周长;
的周长;
(3)若此方程的两根恰好为菱形两条对角线的长,且菱形面积为21,请直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)14;(3)-6
【解析】
(1)先计算判别式的值得△,然后根据判别式的意义得到结论;
(2)先利用解方程得方程的解,分别让一个根为6,求得a的数值,得出方程的根,利用三角形的三边关系判定求得△ABC的周长;
(3)利用菱形的面积等于两条对角线的长的一半建立关于a的方程求得答案即可.
(1)证明:△=[2(a-1)]2-4(a2-a)=-4a+4,
∵a<0,
∴△>0,
∴方程有两个不相等的实数根;
(2)x2+2(a-1)x+(a2-a)=0,
解得:x1=1-a+![]() ,x2=1-a-
,x2=1-a-![]() ,
,
∵等腰△ABC的一腰AB长为6,另两边AC,BC的长分别是这两个方程两个不相等的实数根,
∴当1-a+![]() =6,解得a=-3或-8,则1-a-
=6,解得a=-3或-8,则1-a-![]() =2,
=2,
∴等腰△ABC的周长=6+6+2=14;
(3)∵由根与系数的关系可知两根的积为(a2-a),
∴![]() (a2-a)=21
(a2-a)=21
解得:a=7(不合题意,舍去)或a=-6,
因此a的值是-6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,有下列结论:①
的延长线上,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
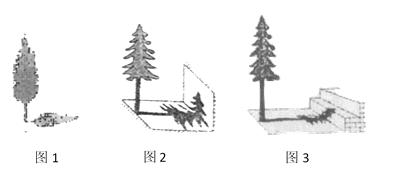
【题目】在“测量物体的高度” 活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4米(如图1).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.3米,一级台阶高为0.3米,落在地面上的影长为4.5米.
(1)在横线上直接填写甲树的高度为 米.
(2)求出乙树的高度.
(3)请选择丙树的高度为( )
A、6.5米 B、5. 5米 C、6.3米 D、4.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
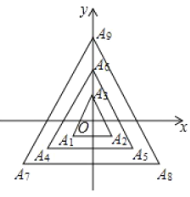
【题目】如图, A1A2 A3 , A4 A5 A6 , A7 A8 A9 ,![]() , A3n2 A3n1A3n(n 为正整数)均为等边三角形,它们的边长依次是 2,4,6,
, A3n2 A3n1A3n(n 为正整数)均为等边三角形,它们的边长依次是 2,4,6,![]() ,2n,顶点 A3,A6,A9,A3n 均在 y 轴上,点 O 是所有等边三角形的中心,点 A2020的坐标为_________.
,2n,顶点 A3,A6,A9,A3n 均在 y 轴上,点 O 是所有等边三角形的中心,点 A2020的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点
的图象开口向上,图象经过点![]() 和
和![]() ,且与
,且与![]() 轴相交于负半轴,给出五个结论:①
轴相交于负半轴,给出五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
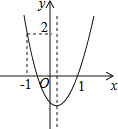
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
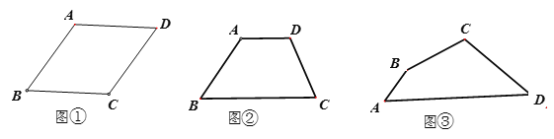
如图①菱形ABCD中,AB=4,∠ABC=60°点0是菱形ABCD两条对角线的交点,EF是经过点O的任意一条线段,容易知道线段EF将菱形ABCD的面积等分,那么线段EF的长度的最大值是 ,最小值是 。
问题探究:
如图② 四边形ABCD中,AD∥BC,AD=2,BC=4,∠B=∠C=60°,请你过点D画出将四边形ABCD面积平分的线段DE,并求出DE的长。
问题解决:
如图③.四边形ABCD是西安城区改造过程中一块不规则空地,为了美化环境,市规划办决定在这块地里种两种花弃,打算过点C修一条笔直的通道,以方便市民出行和观赏花卉,并要求通道两侧种植的花卉面积相等,经测量AB=20米,AD=100米,∠A=60°,∠ABC=150°,∠BCD=120°,若将通道记为CF,请你画出通道CF,并求出通道CF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AD是△ABC的中线,G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x、y≠0).
(1)如图1,若点G与D重合,△ABC为等边三角形,且∠BDE=30°,证明:△AEF∽△DEA;
(2)如图2,若点G与D重合,证明:![]() =2;
=2;
(3)如图3,若AG=nAD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.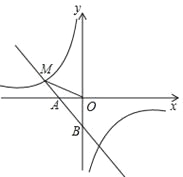
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com