
【题目】AD是△ABC的中线,G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x、y≠0).
(1)如图1,若点G与D重合,△ABC为等边三角形,且∠BDE=30°,证明:△AEF∽△DEA;
(2)如图2,若点G与D重合,证明:![]() =2;
=2;
(3)如图3,若AG=nAD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.

【答案】(1)见解析;(2)见解析;(3)n=![]()
【解析】
(1)先判断出∠BAD=30°,再判断出∠F=30°=∠BAD,即可得出结论;
(2)过C作CH∥AB交EF于H,先判断出△DEB≌△DHC,得出CH=BE,再判断出△FCH∽△FAE,即可得出结论;
(3)先判断出点E是AB的中点,进而得出DE是△ABC的中位线,得出DE=![]() AC,DE∥AC,进而得出△DGE∽△AGF,即可得出结论.
AC,DE∥AC,进而得出△DGE∽△AGF,即可得出结论.
解:(1)∵△ABC为等边三角形,
∴∠BAC=∠B=60°,AB=AC,
∵AD是△ABC的中线,
∴∠BAD=![]() ∠BAC=30°,
∠BAC=30°,
∵∠BDE=30°,
∴EF⊥AB,
∴∠F=30°=∠BAD,
∵∠AED=∠FEA=90°,
∴△AEF∽△DEA;
(2)如图2,过C作CH//AB交EF于H,
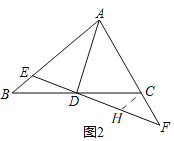
∴∠B=∠DCH,∠BED=∠CHD,
∵AD是△ABC的中线,
∴BD=CD,
∴△DEB≌△DHC(AAS),
∴CH=BE,
∵CH//AB,
∴△FCH∽△FAE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =1﹣
=1﹣![]() =1﹣
=1﹣![]() ,
,![]() =
=![]() ﹣1=
﹣1=![]() ﹣1
﹣1
∴1﹣![]() =
=![]() ﹣1,
﹣1,
∴![]() +
+![]() =2;
=2;
(3)如图3,
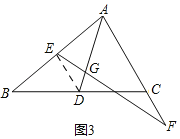
∵y=![]() ,
,
∴AF=![]() AC,
AC,
∴AC=![]() AF,
AF,
∵x=![]() ,
,
∴AE=![]() AB,
AB,
∴点E是AB的中点,
∵AD是△ABC的中线,
∴点D是BC的中点,
∴DE=![]() AC=
AC=![]()
![]() AF=
AF=![]() AF,DE∥AC,
AF,DE∥AC,
∴△DGE∽△AGF,
∴![]() =
=![]() ,
,
∴DG=![]() AG,
AG,
∴AD=AG+DG=AG+![]() AG=
AG=![]() AG,
AG,
∴AG=![]() AD=nAD,
AD=nAD,
∴n=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() ,其中
,其中![]() .
.
(1)求证:此方程有两个不相等的实数根;
(2)若等腰![]() 的一腰
的一腰![]() 长为6,另两边
长为6,另两边![]() ,
,![]() 的长分别是这两个方程两个不相等的实数根,求等腰
的长分别是这两个方程两个不相等的实数根,求等腰![]() 的周长;
的周长;
(3)若此方程的两根恰好为菱形两条对角线的长,且菱形面积为21,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
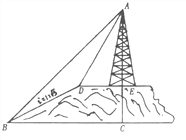
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程a(x﹣h+1)2+k+2=0(a>0)的解是x1=﹣5,x2=1,则不等式a(x+h﹣2)2+k<﹣2的解集为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AE是△ABC的角平分线.AE的垂直平分线交AB于点O,以点O为圆心,OA为半径作⊙O,交AB于点F.
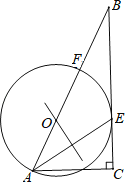
(1)求证:BC是⊙O的切线;
(2)若AC=2,tanB![]() ,求⊙O的半径r的值.
,求⊙O的半径r的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )
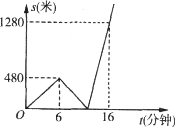
A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
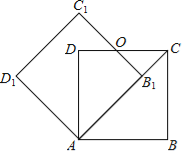
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
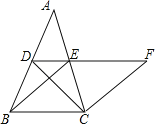
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
(1)求证:四边形BCFE是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com