
【题目】关于x的一元二次方程a(x﹣h+1)2+k+2=0(a>0)的解是x1=﹣5,x2=1,则不等式a(x+h﹣2)2+k<﹣2的解集为_____.
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点
的图象开口向上,图象经过点![]() 和
和![]() ,且与
,且与![]() 轴相交于负半轴,给出五个结论:①
轴相交于负半轴,给出五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
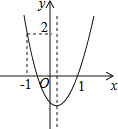
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
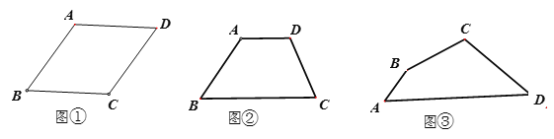
如图①菱形ABCD中,AB=4,∠ABC=60°点0是菱形ABCD两条对角线的交点,EF是经过点O的任意一条线段,容易知道线段EF将菱形ABCD的面积等分,那么线段EF的长度的最大值是 ,最小值是 。
问题探究:
如图② 四边形ABCD中,AD∥BC,AD=2,BC=4,∠B=∠C=60°,请你过点D画出将四边形ABCD面积平分的线段DE,并求出DE的长。
问题解决:
如图③.四边形ABCD是西安城区改造过程中一块不规则空地,为了美化环境,市规划办决定在这块地里种两种花弃,打算过点C修一条笔直的通道,以方便市民出行和观赏花卉,并要求通道两侧种植的花卉面积相等,经测量AB=20米,AD=100米,∠A=60°,∠ABC=150°,∠BCD=120°,若将通道记为CF,请你画出通道CF,并求出通道CF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
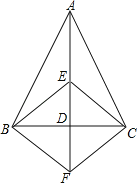
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.
(1)求证:△BDF≌△CDE;
(2)当ED与BC满足什么数量关系时,四边形BECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AD是△ABC的中线,G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x、y≠0).
(1)如图1,若点G与D重合,△ABC为等边三角形,且∠BDE=30°,证明:△AEF∽△DEA;
(2)如图2,若点G与D重合,证明:![]() =2;
=2;
(3)如图3,若AG=nAD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
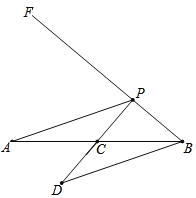
【题目】如图,已知线段AB=6cm,过点B做射线BF且满足∠ABF=40°,点C为线段AB中点,点P为射线BF上的动点,连接PA,过点B作PA的平行线交射线PC于点D,设PB的长度为xcm,PD的长度为y1cm,BD的长度为y2cm.(当点P与点B重合时,y1与y2的值均为6cm)
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x (0≤x≤6)的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.0 | 4.7 | 3.9 | 4.1 | 5.1 | 6.6 | 8.4 |
y2/cm | 6.0 | 5.3 | 4.7 | 4.2 | 3.9 | 4.1 |
(说明:补全表格时相关数值保留一位小数)
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出y1,y2的图象;
(3)结合函数图象解决问题:当△PDB为等腰三角形时,则BP的长度约为 cm;
(4)当x>6时,是否存在x的值使得△PDB为等腰三角形 (填“是”或者“否”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
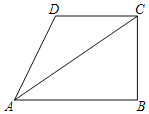
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,连接AC,∠DAC=∠BAC.
(1)求证:AD=DC;
(2)若∠D=120°,求∠ACB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com