
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

【答案】(1) P,Q两点从出发开始到3.2秒时,四边形APQD为长方形; (2) P,Q两点从出发开始到5秒时,四边形PBCQ的面积为33cm2;(3) P,Q两点从出发开始到1.6秒或4.8秒时,点P和点Q的距离是10cm.
【解析】
(1)当PB=CQ时,四边形PBCQ为矩形,依此建立方程求出即可;
(2)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,则PB=(16-3x)cm,QC=2xcm,根据梯形的面积公式可列方程:![]() ,解方程可得解;
,解方程可得解;
(3)作QE⊥AB,垂足为E,设运动时间为x秒,用x表示线段长,用勾股定理列方程求解.
(1)设P,Q两点从出发开始到x秒时,四边形APQD为长方形,
根据题意得:16﹣3x=2x,
解得:x=![]() .
.
答:P,Q两点从出发开始到![]() 秒时,四边形APQD为长方形.
秒时,四边形APQD为长方形.
(2)设P,Q两点从出发开始到y秒时,四边形PBCQ的面积为33cm2,
根据题意得:![]() ×6(16﹣3x+2x)=33,
×6(16﹣3x+2x)=33,
解得:x=5.
答:P,Q两点从出发开始到5秒时,四边形PBCQ的面积为33cm2.
(3)过点Q作QE⊥AB于点E,如图所示.
设P,Q两点从出发开始到x秒时,点P和点Q的距离是10cm,
根据题意得:(16﹣3x﹣2x)2+62=102,
整理得:(16﹣5x)2=82,
解得:x1=![]() ,x2=
,x2=![]() .
.
答:P,Q两点从出发开始到![]() 秒或
秒或![]() 秒时,点P和点Q的距离是10cm.
秒时,点P和点Q的距离是10cm.



科目:初中数学 来源: 题型:
【题目】圆心O到直线l的距离为d,![]() 的半径为R,若d,R是方程
的半径为R,若d,R是方程![]() 的两个根,则直线和圆的位置关系是________;若d,R是方程
的两个根,则直线和圆的位置关系是________;若d,R是方程![]() 的两个根,则
的两个根,则![]() ________时,直线与圆相切.
________时,直线与圆相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
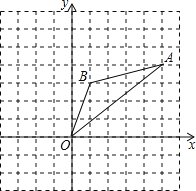
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为______;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCO的顶点O在坐标远点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图像经过点A则K的值是()
的图像经过点A则K的值是()
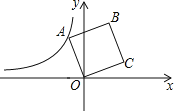
A.-2B.-4C.-8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,DE垂直平分AB,交线段BC于点E(点E与点C不重合),点F为AC上一点,点G为AB上一点(点G与点A不重合),且
,DE垂直平分AB,交线段BC于点E(点E与点C不重合),点F为AC上一点,点G为AB上一点(点G与点A不重合),且![]() .
.
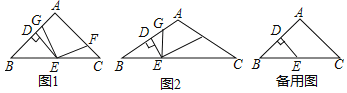
(1)如图1,当![]() 时,线段AG和CF的数量关系是 .
时,线段AG和CF的数量关系是 .
(2)如图2,当![]() 时,猜想线段AG和CF的数量关系,并加以证明.
时,猜想线段AG和CF的数量关系,并加以证明.
(3)若![]() ,
,![]() ,
,![]() ,请直接写出CF的长.
,请直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
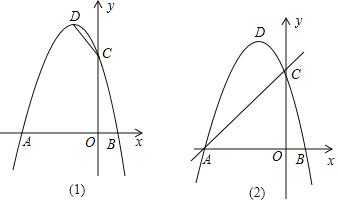
(1)求出点A,C,D的坐标;
(2)如图(1),在抛物线对称轴上找一点E,使得△CBE的周长最小,求点E的坐标;
(3)如图(2),作垂直x轴的直线,在第二象限交直线AC于点M,交抛物线于点N,求当MN有最大值时N点坐标?并求出MN最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com