
【题目】圆心O到直线l的距离为d,![]() 的半径为R,若d,R是方程
的半径为R,若d,R是方程![]() 的两个根,则直线和圆的位置关系是________;若d,R是方程
的两个根,则直线和圆的位置关系是________;若d,R是方程![]() 的两个根,则
的两个根,则![]() ________时,直线与圆相切.
________时,直线与圆相切.
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣5x+4与x轴交于点A,B,与y轴交于点C,顶点为点P.
(1)求△ABP的面积;
(2)在该抛物线上是否存在点Q,使S△ABQ=8S△ABP?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是AC上一点,E是BD上一点,∠A=∠CBD=∠DCE.
(1)求证:△ABC∽△CDE;
(2)若BD=3DE,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
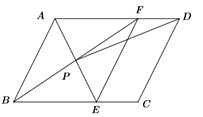
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
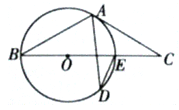
【题目】如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C
(I)若∠ADE=25°,求∠C的度数
(II)若AB=AC,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
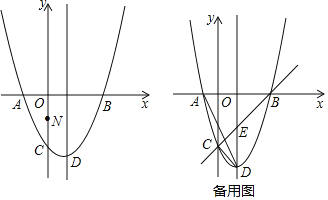
(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴负半轴上的一点,且
轴负半轴上的一点,且![]() ,点
,点![]() 在对称轴右侧的抛物线上运动,连接
在对称轴右侧的抛物线上运动,连接![]() ,
,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,请直接写出
是坐标平面内一点,请直接写出![]() 与
与![]() 全等时点
全等时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)经过点A(1,0)和点B(0,﹣2),且顶点在第三象限,记m=a﹣b+c,则m的取值范围是( )
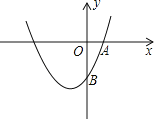
A. ﹣1<m<0B. ﹣2<m<0C. ﹣4<m<﹣2D. ﹣4<m<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com