
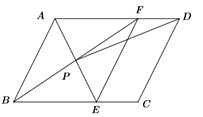
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求PD.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由四边形ABCD是平行四边形,得到AD∥BC,从而得到∠AFB=∠FBE,再由∠ABF=∠FBE,推出∠ABF=∠AFB,于是得到AB=AF,同理得出AB=BE,于是得出结论;
(2)由菱形的性质得出AE⊥BF,得到∠ABF=30°,∠BAP=∠FAP=60°从而得出AP=2,过点P作PM⊥AD于M,得到PM=![]() ,AM=1,DM=5,然后利用勾股定理求PD即可.
,AM=1,DM=5,然后利用勾股定理求PD即可.
(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AFB=∠FBE.
∵∠ABF=∠FBE,∴∠ABF=∠AFB,∴AB=AF,同理AB=BE,∴四边形ABEF是菱形;
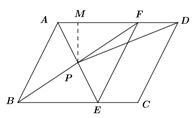
(2)∵四边形ABEF是菱形,∴AE⊥BF.
∵∠ABC=60°,∴∠ABF=30°,∠BAP=∠FAP=60°.
∵AB=4,∴AP=2,如图,过点P作PM⊥AD于M,∴PM=![]() ,AM=1.
,AM=1.
∵AD=6,∴DM=5,∴PD=![]() .
.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是( )
A. 抛物线与x轴的一个交点为(4,0)
B. 函数y=ax2+bx+c的最大值为6
C. 抛物线的对称轴是x=![]()
D. 在对称轴右侧,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
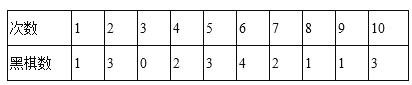
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚B. 50枚C. 40枚D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
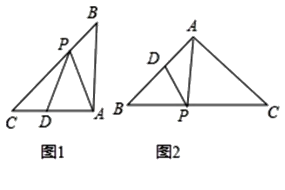
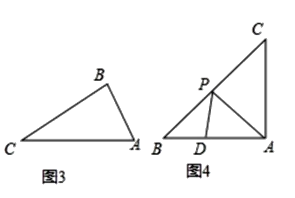
【题目】如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.
(1)如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是___;
(2)如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;
(3)如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”,请写出AD长度的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆心O到直线l的距离为d,![]() 的半径为R,若d,R是方程
的半径为R,若d,R是方程![]() 的两个根,则直线和圆的位置关系是________;若d,R是方程
的两个根,则直线和圆的位置关系是________;若d,R是方程![]() 的两个根,则
的两个根,则![]() ________时,直线与圆相切.
________时,直线与圆相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
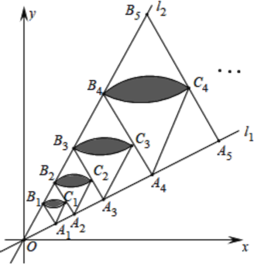
【题目】如图,直线![]() 的解析式是
的解析式是![]() ,直线
,直线![]() 的解析式是
的解析式是![]() ,点
,点![]() 在
在![]() 上,
上,![]() 的横坐标为
的横坐标为![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() ,
,![]() 为邻边在直线
为邻边在直线![]() ,
,![]() 间作菱形
间作菱形![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,以
为圆心,以![]() 为半径画弧得扇形
为半径画弧得扇形![]() 和扇形
和扇形![]() ,记扇形
,记扇形![]() 与扇形
与扇形![]() 重叠部分的面积为
重叠部分的面积为![]() ;延长
;延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() ,
,![]() 为邻边在
为邻边在![]() ,
,![]() 间作菱形
间作菱形![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,以
为圆心,以![]() 为半径画弧得扇形
为半径画弧得扇形![]() 和扇形
和扇形![]() ,记扇形
,记扇形![]() 与扇形
与扇形![]() 重叠部分的面积为
重叠部分的面积为![]() 按照此规律继续作下去,则
按照此规律继续作下去,则![]() __.(用含有正整数
__.(用含有正整数![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,与反比例函数的图象交于点C,连接CO,过C作CD⊥x轴于D,已知tan∠ABO=![]() ,OB=4,OD=2.
,OB=4,OD=2.
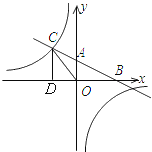
(1)求直线AB和反比例函数的解析式;
(2)在x轴上有一点E,使△CDE与△COB的面积相等,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCO的顶点O在坐标远点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图像经过点A则K的值是()
的图像经过点A则K的值是()
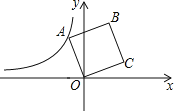
A.-2B.-4C.-8D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com