
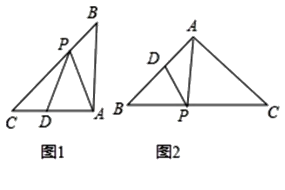
����Ŀ����ͼ1������ABC�У���BC����ȡһ��P����AC����ȡһ��D����AP��PD�������APD�ǵ�������������ABP����CDP���ƣ����dz���APD��AC���ϵ���������������������.
(1)��ͼ2,����ABC��AB=AC,��B=50������APD��AB���ϵ�������������������������AD=DP����PAC=��BPD�����PAC�Ķ�����___��
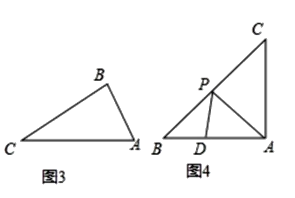
(2)��ͼ3������ABC�У���A=2��C����AC�������ٴ���һ����������������APD�����뻭��һ��AC���ϵ���������������APD������˵�����ɣ�
(3)��ͼ4����Rt��ABC��AB=AC=2����APD��AB���ϵ�������������������������д��AD���ȵ����п���ֵ.
���𰸡���1��30������2������������3��AD�ij�Ϊ1��![]() ��
��![]() .
.
��������
��1�����ݵȱ߶ԵȽǺ���������ǵ�����֤����B����PAB���ɽ�����⣮
��2����ͼ3�У�����BAC��ƽ����AP��BC��P����PD��AB��AC��D������ƽ���ߵ����ʺͽ�ƽ���߶���ɵá�BAP=��PAD=��DPA����CPD=��B����ϡ�A=2��C��֤��APD�ǵ�������������APB����CDP���ƣ����ɽ�����⣮
��3���������������ۣ���ͼ3���У���DA��DPʱ����ͼ4�У���PA��PDʱ����ͼ5�У���AP��ADʱ���ֱ���⼴�ɽ�����⣮
�⣺��1����ͼ2�У�
��AB��AC��DA��DP��
���B����C����DAP����DPA��
�ߡ�PAC����BPD��
���APC����BDP����DAP����DPA��
�ߡ�APC����B����BAP��
���B����PAB��50����
�ߡ�BAC��180��50��50����80����
���PAC��30��
�ʴ�Ϊ30����
��2����ͼ3�У���APD��AC���ϵ�����������������������
���ɣ�����BAC��ƽ����AP��BC��P����PD��AB��AC��D��
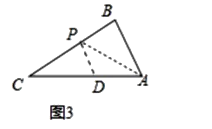
���BAP=��PAD=��DPA����CPD=��B��
��DP=DA��
�ߡ�CAB=2��C��
���BAP =��C��
���APD�ǵ����������ҡ�APB���CDP���ƣ�
���APD��AC���ϵ�����������������������
��3����ͼ3���У���DA=DPʱ�����APD=��DAP=x��
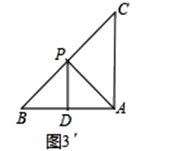
������BPD=��CAP=90��-x����BDP=��CPA=2x��
��90��-x+2x+x=180����
��x=45����
�������ζ��ǵ���ֱ�������Σ���֪AD=1��
������PDB=��CAPʱ�����APD=��DAP=x��
�õ���PDB=��CAP=2x����֪x=30����
��AD=a����AP=![]()
�ߡ�BPD�ס�CPA��
��![]() ����
����![]() ��
��
���![]() ��
��
��ͼ4�У���PA=PDʱ����֪��PDB�Ƕ۽ǣ���CAP����ǣ�
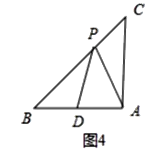
���PDB=��CPA�����BPD�ա�CPA��
��AD=a����BD=2-a��![]() ��AC=2��
��AC=2��
![]() ��
��
���a=![]() ��
��
��ͼ5�У���AP=ADʱ�����APD=��ADP=x�����DAP=180��-2x����֪��PDBΪ�۽ǣ���CAPΪ��ǣ�
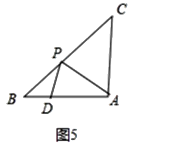
���PDB=��CPA=180��-x����CAP=90��-��DAP=90��-��180��-2x��=2x-90����
�ڡ�APC�У�2x-90��+180��-x+45��=180����
���x=45���������ܳ�����
����������AD�ij�Ϊ1��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס�������ͬѧ��ѡ��һ�˲μӡ��л���ʫ�ʡ�����������ͬ�IJ��������£�����![]() �β��Գɼ�(��λ����)���£�
�β��Գɼ�(��λ����)���£�
�ף�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ң�
�ң�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ش��������⣺
(1)�׳ɼ���ƽ������ ���ҳɼ���ƽ������ ��
(2)����Ӽס�������![]() �εijɼ��и������ȡһ�γɼ����з�������鵽�������˵ijɼ�������
�εijɼ��и������ȡһ�γɼ����з�������鵽�������˵ijɼ�������![]() �ֵĸ���.(���б�����״ͼ�ķ���)
�ֵĸ���.(���б�����״ͼ�ķ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ�������ֱ���O��0��0����A��3��0����B��4��4����C��-2��3��������O��A��B��C�ĺ����ꡢ�����궼����-2.
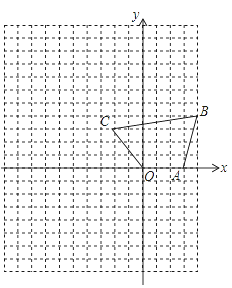
(1)�����Ա仯����ĸ���Ϊ������ı��Σ�
(2)�ɣ�1���õ����ı������ı���OABCλ�������λ�ƣ�ָ��λ�����ļ���ԭͼ�ε����Ʊ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2������A(2��1)��
(1)����������Ľ���ʽ��
(2)����������ͼ��д���������ϵ�A����y ��ĶԳƵ�B �����ꣻ
(3)���������Ƿ���ڵ�C��ʹ��ABC��������ڡ�OAB�����һ�룬�����ڣ����C������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
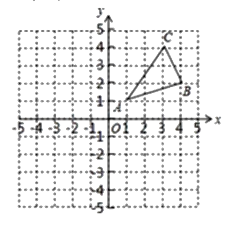
����Ŀ����ͼ���������������ֱ�ΪA(1,1),B(4,2),C(3,4);
(1)�뻭������A����ʱ����ת90�ȵõ���ͼ����AB1C1��
(2)�뻭������ԭ��O�����ĶԳƵ�ͼ��![]() ��
��
(3)��x������һ��P��ʹPA+PB��ֵ��С������ͼ�ϱ����P����ֱ��д����P������______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
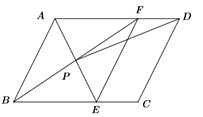
����Ŀ����ͼ����ƽ���ı���ABCD�У�AEƽ�֡�BAD����BC�ڵ�E��BFƽ�֡�ABC����AD�ڵ�F��AE��BF���ڵ�P������EF��PD��
��1����֤���ı���ABEF�����Σ�
��2����AB=4��AD=6����ABC=60������PD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
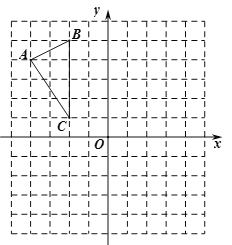
����Ŀ����ͼ��![]() ��ƽ��ֱ������ϵ�ڣ����������ֱ�Ϊ
��ƽ��ֱ������ϵ�ڣ����������ֱ�Ϊ![]() ��
��![]() ��
��![]() .
.
��1��ƽ��![]() ��ʹ��
��ʹ��![]() �Ƶ���
�Ƶ���![]() ������ƽ�ƺ��
������ƽ�ƺ��![]() ����д����
�������![]() ������.
������.
��2����![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() ���õ�
���õ�![]() ��������ת���
��������ת���![]() ����д����
�������![]() ������.
������.
��3����2���еĵ�![]() ��ת����
��ת����![]() ʱ����
ʱ����![]() ������·�������������
������·�������������![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2+bx+2��ͼ����x���ཻ�ڵ�A����1��0����B��4��0������y���ཻ�ڵ�C��

��1����ú����ı���ʽ��
��2����PΪ�ú����ڵ�һ�����ڵ�ͼ����һ�㣬����P��PQ��BC������Ϊ��Q������PC��
�����߶�PQ�����ֵ��
�����Ե�P��C��QΪ��������������ABC���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
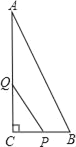
����Ŀ����ͼ����ABC�У���C��90����AC��16cm��BC��8cm��һ����P�ӵ�C��������CB������2cm/s���ٶ��˶�����һ����Q��A��������AC����4cm/s���ٶ��˶���P��Q����ͬʱ�������˶�ʱ��Ϊt��s����
��1������PCQ���������ABC�����![]() ����t��ֵ��
����t��ֵ��
��2����PCQ������ܷ����ı���ABPQ�����ȣ����ܣ����t��ֵ�������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com