
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )
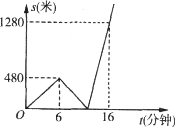
A.1300 米B.1400 米C.1600 米D.1500 米
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若一次函数ymxn与反比例函数y![]() 同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
(1)判断y2x1与y![]() 是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
(2)已知:整数m,n,t满足条件t<n<8m,并且一次函数y=(1+n)x+2m+2与反比例函数y![]() 存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
(3)若一次函数yxm和反比例函数y![]() 在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
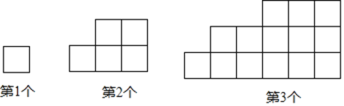
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批学习笔记本,已知1本甲种笔记本和3本乙种笔记本共需26元;3本甲种笔记本和2本乙种笔记本共需29元.
(1)求购买一本甲种笔记本和一本乙种笔记本各需多少元;
(2)学校计划购进这两种笔记本共70本,并且甲种笔记本的数量不超过乙种笔记本数量的2倍,若设学校计划购进甲种比价本x本.
①填写下表:
甲种笔记本数量 | 10 |
|
乙种笔记本数量 |
| 30 |
所需总费用 |
|
|
②写出购买这两种笔记本所需要费用y(元)关于x的函数关系式;请设计出最省钱的购买方案,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
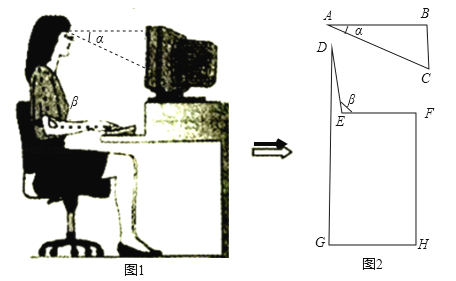
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与![]() 相交,那么r的取值范围是( )
相交,那么r的取值范围是( )
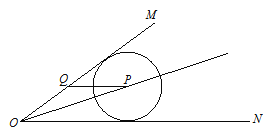
A.4<r<12B.2<r<12C.4<r<8D.r>4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量瀑布![]() 的高度,测量人员在瀑布对面山上的
的高度,测量人员在瀑布对面山上的![]() 点处测得瀑布顶端
点处测得瀑布顶端![]() 点的仰角是
点的仰角是![]() ,测得瀑布底端
,测得瀑布底端![]() 点的俯角是
点的俯角是![]() ,
,![]() 与水平面垂直.又在瀑布下的水平面测得
与水平面垂直.又在瀑布下的水平面测得![]() ,
,![]() (注:
(注:![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() 于点
于点![]() ),斜坡
),斜坡![]() ,坡角
,坡角![]() ,那么瀑布
,那么瀑布![]() 的高度约为( ).(精确到
的高度约为( ).(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
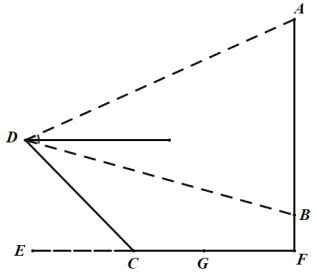
A.![]()
![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.

(1)分别写出两个印刷厂的收费![]() ,
,![]() (元)与印制数量
(元)与印制数量![]() (份)之间的关系式(不用写出自变量的取值范围);
(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一坐标系内画出它们的图象,并求出当印制多少份宣传材料,两个印刷厂的印制费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印制省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
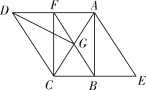
【题目】如图,在ABC中,∠ABC=90°,∠ACB=60°,将ABC绕点C逆时针旋转60°得到DGC,再将ABC沿AB所在直线翻折得到ABE,连接AD,BG,延长BG交AD于点F,连接CF.
(1)求证:四边形ABCF是矩形;
(2)若GF=2![]() ,求四边形AECD的面积.
,求四边形AECD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com