
【题目】如图,在ABC中,∠ABC=90°,∠ACB=60°,将ABC绕点C逆时针旋转60°得到DGC,再将ABC沿AB所在直线翻折得到ABE,连接AD,BG,延长BG交AD于点F,连接CF.
(1)求证:四边形ABCF是矩形;
(2)若GF=2![]() ,求四边形AECD的面积.
,求四边形AECD的面积.
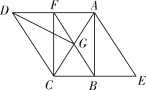
【答案】(1)见解析;(2)24![]()
【解析】
(1)由旋转的性质可得AC=CD,∠DCG=∠ACB=60°,CG=CB,可证△ACD是等边三角形,△CBG是等边三角形,可得∠DAC=∠CGB=∠AGF=60°,BG=BC=CG,由直角三角形的性质可得AG=CG=BC,由矩形的判定可得结论;
(2)先证四边形AECD是菱形,由菱形的面积公式可求解.
(1)∵△ABC绕点C旋转得到△DGC,
∴AC=CD,∠DCG=∠ACB=60°,
∴△ACD是等边三角形,
∴∠DAC=60°
∵在Rt△DGC中,∠CDG=30°,
∴DC=2CG=AC,
∴AG=GC=BC,
∴∠CGB=∠AGF=60°,
∴△CBG和△AGF都是等边三角形,
∴AG=GC=BG=GF,
∴四边形ABCF是矩形;
(2)∵△ABC绕点C旋转得到△DGC,△ABC沿AB所在直线翻折得到△ABE,∠ABC=90°,∠ACB=60°,
∴DC=AC=AE,∠DCG=∠ACB=∠AEC=60°,
∴∠AEC+∠DCE=180°,
∴DC∥AE,
∴四边形AECD为平行四边形.
又∵AC=2CB,
∴AC=CE=AE,
∴四边形AECD为菱形
∵GF=2![]() ,
,
∴AC=CE=4![]() ,CB=2
,CB=2![]() ,
,
∴AB=![]() =6,
=6,
∴S四边形AECD=4![]() ×6=24
×6=24![]()


科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )
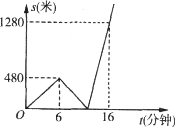
A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
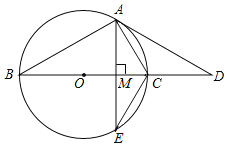
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近段时间成都空气质量明显下降,市场上的空气净化器再次成为热销,某商店经销--种空气净化器,每台净化器的成本价为![]() 元,经过一段时间的销售发现,每月的销售量
元,经过一段时间的销售发现,每月的销售量![]() 台与销售单价
台与销售单价![]() (元)的关系为
(元)的关系为![]() .
.
(1)该商店每月的利润为![]() 元,写出利润
元,写出利润![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)若要使每月的利润为![]() 元,销售单价应定为多少元?
元,销售单价应定为多少元?
(3)商店要求销售单价不低于![]() 元, 也不高于
元, 也不高于![]() 元,那么该商店每月的最高利润和最低利润分别为多少?
元,那么该商店每月的最高利润和最低利润分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
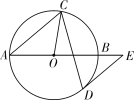
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,用树状图表示或列表法求足球踢到了小华处的概率是多少
(2)如果从小明开始踢,经过踢三次后,球踢到了小明处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AD∥BC,∠B=90°,AD=BC=20,AB=8,动点P从点B出发,先以每秒2cm的速度沿B→A的方向运动,到达点A后再以每秒4cm的速度沿A→D的方向向终点D运动;动点Q从点B出发以每秒2cm的速度沿B→C的方向向终点C运动.其中一个动点到达终点时,另一个动点也随之停止运动,设点P、Q同时出发,运动时间为t秒.
(1)直接写出BQ的长(用含t的代数式表示)
(2)求△BPQ的面积S(用含t的代数式表示)
(3)求当四边形APCQ为平行四边形t的值
(4)若点E为BC中点,直接写出当△BEP为等腰三角形时t的值.
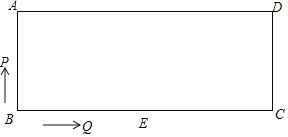
查看答案和解析>>
科目:初中数学 来源: 题型:
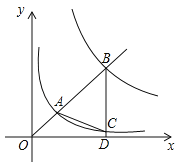
【题目】(2017浙江省湖州市,第16题,4分)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数![]() 和
和![]() 在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交
在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交![]() 的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
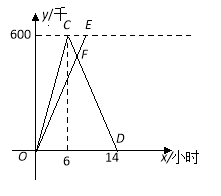
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距100千米时,求甲车行驶的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com