练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是⊙O的直径，弦CD与AB相交，连接CO，过点D作⊙O的切线，与AB的延长线交于点E，若DE∥AC，∠BAC＝40°，则∠OCD的度数为（ ）

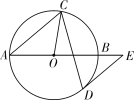
    A.65°B.30°C.25°D.20°

    【答案】C

    【解析】

    连接OD，如图，先利用平行线的性质得∠E=∠BAC=40°，再根据切线的性质得OD⊥DE，则可计算出∠DOE=50°，接着根据圆周角定理得到∠BOC=2∠A=80°．然后根据等腰三角形的性质和三角形内角和计算∠OCD的度数．

    连接OD，如图，


    ∵DE∥AC，
    ∴∠E=∠BAC=40°，
    ∵DE为切线，
    ∴OD⊥DE，
    ∴∠DOE=90°-40°=50°，
    ∵∠BOC=2∠A=80°．
    ∴∠COD=80°+50°=130°，
    ∵OC=OD，
    ∴∠OCD=∠ODC=（180°-130°）=25°．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

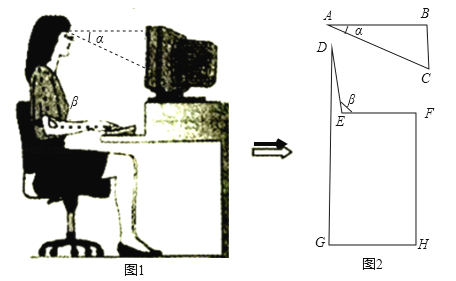
    【题目】（2017江西省）如图1，研究发现，科学使用电脑时，望向荧光屏幕画面的“视线角”α约为20°，而当手指接触键盘时，肘部形成的“手肘角”β约为100°．图2是其侧面简化示意图，其中视线AB水平，且与屏幕BC垂直．

    （1）若屏幕上下宽BC=20cm，科学使用电脑时，求眼睛与屏幕的最短距离AB的长；

    （2）若肩膀到水平地面的距离DG=100cm，上臂DE=30cm，下臂EF水平放置在键盘上，其到地面的距离FH=72cm．请判断此时β是否符合科学要求的100°？

    （参考数据：sin69°≈，cos21°≈，tan20°≈，tan43°≈，所有结果精确到个位）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

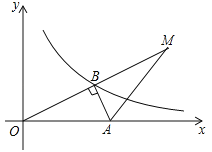
    【题目】如图，在平面直角坐标系中，Rt△AOB的斜边OA在x轴的正半轴上，∠OBA=90°，且tan∠AOB=，OB=，反比例函数的图象经过点B．

    （1）求反比例函数的表达式；

    （2）若△AMB与△AOB关于直线AB对称，一次函数y=mx+n的图象过点M、A，求一次函数的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

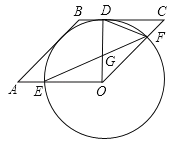
    【题目】已知：四边形OABC是菱形，以O为圆心作⊙O，与BC相切于点D，交OA于E，交OC于F，连接OD，DF．

    （1）求证：AB是⊙O的切线；

    （2）连接EF交OD于点G，若∠C=45°，求证：GF2=DGOE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点是轴正半轴上的一动点，抛物线(是常数，且过点，与轴交于两点，点在点左侧，连接，以为边做等边三角形，点与点在直线两侧．

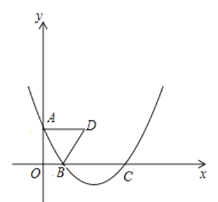
    （1）求B、C的坐标；

    （2）当轴时，求抛物线的函数表达式；

    （3）①求动点所成的图像的函数表达式；

    ②连接，求的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABC中，∠ABC＝90°，∠ACB＝60°，将ABC绕点C逆时针旋转60°得到DGC，再将ABC沿ＡＢ所在直线翻折得到ABE，连接AD，BG，延长BG交AD于点F，连接CF．

    （1）求证：四边形ABCF是矩形；

    （2）若GF＝2，求四边形AECD的面积．

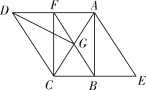
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点M是矩形ABCD的边AD的中点，点P是BC边上一动点，PE⊥MC，PF⊥BM，垂足为E、F．

    (1)当矩形ABCD的长与宽满足什么条件时，四边形PEMF为矩形？猜想并证明你的结论．

    (2)在(1)中，当点P运动到什么位置时，矩形PEMF变为正方形，为什么？

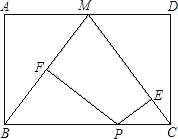
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着网购的日益盛行，物流行业已逐渐成为运输业的主力，已知某大型物流公司有A、B两种型号的货车，A型货车的满载量是B型货车满载量的2倍多4吨，在两车满载的情况下，用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同．

    （1）1辆A型货车和1辆B型货车的满载量分别是多少？

    （2）该物流公司现有120吨货物，可以选择上述两种货车运送，在满载的情况下，有几种方案可以一次性运完？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数 y＝ax2+bx 的图象与 x 轴交于点 O（0，0）和 点 B，抛物线的对称轴是直线 x＝3．点 A 是抛物线在第一象限上的一个动点， 过点 A 作 AC⊥x 轴，垂足为 C．S△AOB＝3S△ABC，AC2＝OCBC．

    （1）求该二次函数的解析式；

    （2）抛物线的对称轴与 x 轴交于点 M．连接 AM，点 N 是线段 OA 上的一点．当 ∠AMN＝∠AOM 时，求点 N 的坐标；

    （3）点 P 是抛物线上的一个动点．点 Q 是 y 轴上的一动点．当以 A，B，P，Q 四个点为顶点的四边形为平行四边形时，直接写出点 P 坐标．

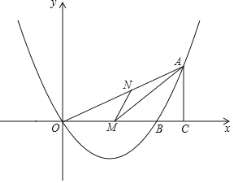
    查看答案和解析>>

    同步练习册答案