
【题目】如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与![]() 相交,那么r的取值范围是( )
相交,那么r的取值范围是( )
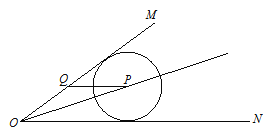
A.4<r<12B.2<r<12C.4<r<8D.r>4
【答案】A
【解析】
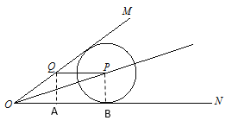
过点Q作QA⊥AN于A,过点P作PB⊥ON于B,得到四边形ABPQ是矩形,QA=PB=4,根据∠MON=30°求出OQ=2QA=8,根据平行线的性质及角平分线的性质得到PQ=8,再分内切与外切两种求出半径r,即可得到两圆相交时的半径r的取值范围.
过点Q作QA⊥AN于A,过点P作PB⊥ON于B,
∵PQ∥ON,
∴PQ⊥PB,
∴∠QAB=∠QPB=∠PBA=90°,
∴四边形ABPQ是矩形,
∴QA=PB=4,
∵∠MON=30°,
∴OQ=2QA=8,
∵OP平分∠MON,PQ∥ON,
∴∠QOP=∠PON=∠QPO,
∴PQ=OQ=8,
当以Q为圆心半径为r的圆与![]() 相外切时,r=8-4=4,
相外切时,r=8-4=4,
当以Q为圆心半径为r的圆与![]() 相内切时,r=8+4=12,
相内切时,r=8+4=12,
∴以Q为圆心半径为r的圆与![]() 相交,4<r<12,
相交,4<r<12,
故选:A.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
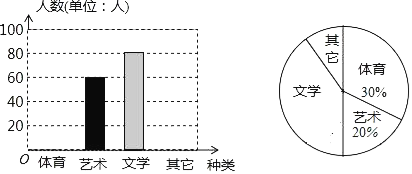
(1)此次共调查了多少人?
(2)求体育社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有3000名学生,请估计喜欢文学类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )
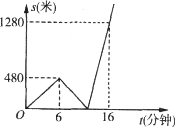
A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,其顶点为C.
,其顶点为C.

(1)求抛物线的解析式和顶点C的坐标;
(2)我们把坐标为(n,m)的点叫做坐标为(m,n)的点的反射点,已知点M在这条抛物线上,它的反射点在抛物线的对称轴上,求点M的坐标;
(3)点P是抛物线在第一象限部分上的一点,如果∠POA=∠ACB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区正在积极创建国家模范卫生城市,学校为了普及学生卫生健康知识,提高学生创卫意识,举办了创卫知识竞赛,以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:75 88 93 65 78 94 89 68 95 50 89 88 89 89 77 95 87 88 92 91
初二:74 96 96 89 97 74 69 76 72 78 99 72 97 85 98 74 89 73 98 74
(1)整理、描述数据:
成绩 |
|
|
|
|
|
初一(频数) | 1 | 2 | 3 |
| 6 |
初二(频数) | 0 | 1 | 9 | 3 | 7 |
(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下不合格)
分析数据:
平均数 | 中位数 | 众数 | |
初一 | 84 |
| 89 |
初二 | 84 | 81.5 |
|
请根据上述的数据,填空:![]() ______;
______;![]() ______;
______;![]() ______;
______;
(2)得出结论:
你认为哪个年级掌握创卫知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
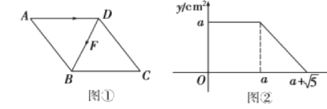
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,用树状图表示或列表法求足球踢到了小华处的概率是多少
(2)如果从小明开始踢,经过踢三次后,球踢到了小明处的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com