
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为正方形的中心,点
为正方形的中心,点![]() 为
为![]() 边上一动点,直线
边上一动点,直线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,则
,则![]() 的最小值为( )
的最小值为( )

A.2B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
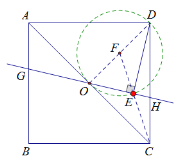
连接OD,AC,取OD中点F,由∠OED=90°可证得点E在以OD中点F为圆心,DF为半径的圆上,进而可知当点C、E、F三点在同一直线上时,CE取最小值,由正方形的性质可得OD=OC=2,进而可得OF=1,最后用勾股定理即可求得CF的长,进而可求得CE的最小值.
解:连接OD,AC,
由题意可知,在正方形中,OD⊥AC,
∵在△ODE中OD的长为定值,∠OED始终为90°,
∴点E在以OD中点F为圆心,OD为直径的圆上,
连接EF,CE,当点C、E、F三点在同一直线上时,CE取最小值,
∵正方形的边长为![]() ,点O为正方形中心,
,点O为正方形中心,
∴![]() ,
,
∴![]() ,
,
∴在Rt△ABC中,![]() ,
,
∴CE的最小值为![]()
故选:D.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
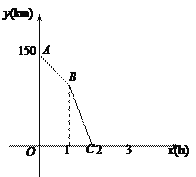
【题目】一辆货车从甲地出发以50 km/h的速度匀速驶往乙地,行驶1 h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8 h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)甲乙两地之间的距离是__________ km,轿车的速度是_________ km/h;
(2)求线段BC所表示的函数表达式;
(3)在图中画出货车与轿车相遇后的y(km)与x(h)的函数图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
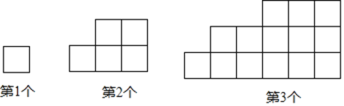
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
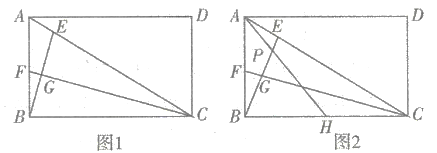
【题目】如图,在矩形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一动点,连接
上一动点,连接![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() 于点
于点 ![]() .
.
(1)如图1,若![]() 恰好平分
恰好平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于点
于点 ![]() .
.
求证:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批学习笔记本,已知1本甲种笔记本和3本乙种笔记本共需26元;3本甲种笔记本和2本乙种笔记本共需29元.
(1)求购买一本甲种笔记本和一本乙种笔记本各需多少元;
(2)学校计划购进这两种笔记本共70本,并且甲种笔记本的数量不超过乙种笔记本数量的2倍,若设学校计划购进甲种比价本x本.
①填写下表:
甲种笔记本数量 | 10 |
|
乙种笔记本数量 |
| 30 |
所需总费用 |
|
|
②写出购买这两种笔记本所需要费用y(元)关于x的函数关系式;请设计出最省钱的购买方案,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
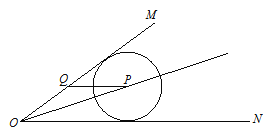
【题目】如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与![]() 相交,那么r的取值范围是( )
相交,那么r的取值范围是( )
A.4<r<12B.2<r<12C.4<r<8D.r>4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
①abc>0; ②3a+b>0; ③﹣1<k<0; ④4a+2b+c<0; ⑤a+b<k.

A. ①②③ B. ②③⑤
C. ②④⑤ D. ②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com