
【题目】如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
①abc>0; ②3a+b>0; ③﹣1<k<0; ④4a+2b+c<0; ⑤a+b<k.

A. ①②③ B. ②③⑤
C. ②④⑤ D. ②③④⑤
【答案】B
【解析】试题解析:∵抛物线开口向上,
∴a>0.
∵抛物线对称轴是x=1,
∴b<0且b=-2a.
∵抛物线与y轴交于正半轴,
∴c>0.
∴①abc>0错误;
∵b=-2a,
∴3a+b=3a-2a=a>0,
∴②3a+b>0正确;
∵b=-2a,
∴4a+2b+c=4a-4a+c=c>0,
∴④4a+2b+c<0错误;
∵直线y=kx+c经过一、二、四象限,
∴k<0.
∵OA=OD,
∴点A的坐标为(c,0).
直线y=kx+c当x=c时,y>0,
∴kc+c>0可得k>-1.
∴③-1<k<0正确;
∵直线y=kx+c与抛物线y=ax2+bx+c的图象有两个交点,
∴ax2+bx+c=kx+c,
得x1=0,x2=![]()
由图象知x2>1,
∴![]() >1
>1
∴k>a+b,
∴⑤a+b<k正确,
即正确命题的是②③⑤.
故选B.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是![]() 中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E

(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() x2+x+4.
x2+x+4.
(1)确定抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
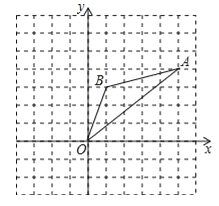
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为 ;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(![]() ,0),点B在抛物线
,0),点B在抛物线![]() 上.
上.

(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的解析式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com