
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(![]() ,0),点B在抛物线
,0),点B在抛物线![]() 上.
上.

(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的解析式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由。
【答案】(1)A(0,2),B(![]() ,1).
,1).
(2)![]() .
.
(3)15/8
(4)存在,
点P的坐标为(1,-1)和(2,1)
【解析】(1)A(0,2),B(![]() ,1).
,1).
(2)![]() .
.
(3)如图1,可求得抛物线的顶点D(![]() ).
).
设直线BD的关系式为![]() , 将点B、D的坐标代入,求得
, 将点B、D的坐标代入,求得![]() ,
, ![]() ,
,
∴BD的关系式为![]() .
.
设直线BD和x轴交点为E,则点E(![]() ,0),CE=
,0),CE=![]() .
.
∴ △DBC的面积为![]() .
.
(4)存在,
点P的坐标为(1,-1)和(2,1)
(1)根据腰长为![]() 的等腰Rt△ABC(∠C=90°),由AC=
的等腰Rt△ABC(∠C=90°),由AC=![]() ,CO=1,求出AO即可得出A点的坐标,进而得出B点的坐标;
,CO=1,求出AO即可得出A点的坐标,进而得出B点的坐标;
(2)将B点坐标代入y=ax2+ax-2即可得出二次函数解析式;
(3)由(2)得顶点D的坐标,从而求得BD的关系式,设直线BD和x轴交点为E,可求得E点坐标,求得CE长,最后求得△DBC的面积
(4)延长BC到P,使CP=BC,连接AP,利用等腰直角三角形的性质与全等三角形的判定与性质解答即可.


科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
①abc>0; ②3a+b>0; ③﹣1<k<0; ④4a+2b+c<0; ⑤a+b<k.

A. ①②③ B. ②③⑤
C. ②④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
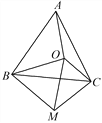
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
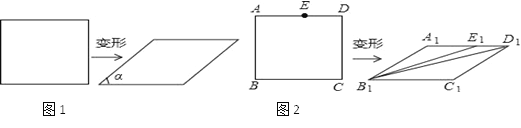
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把![]() 的值叫做这个平行四边形的变形度.
的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, ![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AEAD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4![]() (m>0),平行四边形A1B1C1D1的面积为2
(m>0),平行四边形A1B1C1D1的面积为2![]() (m>0),试求∠A1E1B1+∠A1D1B1的度数.
(m>0),试求∠A1E1B1+∠A1D1B1的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com