
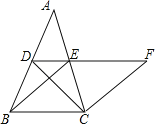
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
(1)求证:四边形BCFE是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).
【答案】(1)证明见解析;(2)△FEC、△AEB、△ADC、△BDC.
【解析】
(1)结合三角形中位线的性质先证明四边形BCFE是平行四边形,再得出邻边BC=BE,则四边形BCFE是菱形;
(2)根据平行线的性质、三角形的面积公式解答即可.
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC,BC=2DE.
∵CF∥BE,
∴四边形BCFE是平行四边形.
∵BE=2DE,BC=2DE,
∴BE=BC.
∴四边形BCFE是菱形;
(2)解:①∵由(1)知,四边形BCFE是菱形,
∴BC=FE,BC∥EF,
∴△FEC与△BEC是等底等高的两个三角形,
∴S△FEC=S△BEC.
②∵E为AC的中点,∴△AEB与△BEC是等底同高的两个三角形,则S△AEB=S△BEC.
③∵D为AB的中点,∴S△ADC=S△BDC=![]() S△ABC,又S△BEC=
S△ABC,又S△BEC=![]() S△ABC,则S△ADC=S△BDC=S△BEC.
S△ABC,则S△ADC=S△BDC=S△BEC.
综上所述,与△BEC面积相等的三角形有:△FEC、△AEB、△ADC、△BDC.


科目:初中数学 来源: 题型:
【题目】AD是△ABC的中线,G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x、y≠0).
(1)如图1,若点G与D重合,△ABC为等边三角形,且∠BDE=30°,证明:△AEF∽△DEA;
(2)如图2,若点G与D重合,证明:![]() =2;
=2;
(3)如图3,若AG=nAD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.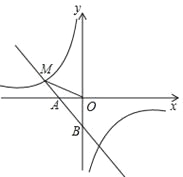
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一抛物线的顶点坐标是
中,一抛物线的顶点坐标是![]() ,且过点
,且过点![]() ,平行四边形
,平行四边形![]() 的顶点在
的顶点在![]() 此抛物线上,
此抛物线上,![]() 与
与![]() 轴相交于点
轴相交于点![]() .己知点
.己知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是抛物线上任意一点.
是抛物线上任意一点.
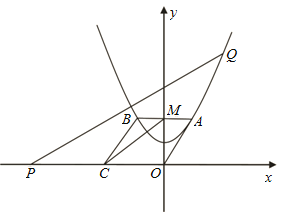
(1)求此抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在抛物线上是否存在点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍?若存在,求此时点
的面积的2倍?若存在,求此时点![]() 的坐标.
的坐标.
(3)在![]() 轴上有一动点
轴上有一动点![]() ,若
,若![]() ,试建立
,试建立![]() 关于
关于![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的运动范围;
的运动范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
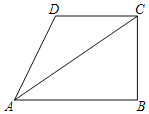
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,连接AC,∠DAC=∠BAC.
(1)求证:AD=DC;
(2)若∠D=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.
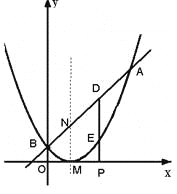
(1)求m的值及这个二次函数的解析式;
(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
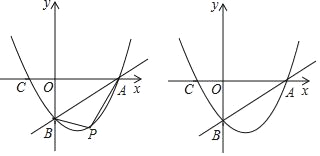
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
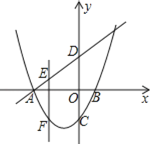
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com