
【题目】如图,在平面直角坐标系![]() 中,一抛物线的顶点坐标是
中,一抛物线的顶点坐标是![]() ,且过点
,且过点![]() ,平行四边形
,平行四边形![]() 的顶点在
的顶点在![]() 此抛物线上,
此抛物线上,![]() 与
与![]() 轴相交于点
轴相交于点![]() .己知点
.己知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是抛物线上任意一点.
是抛物线上任意一点.
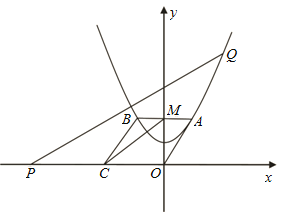
(1)求此抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在抛物线上是否存在点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍?若存在,求此时点
的面积的2倍?若存在,求此时点![]() 的坐标.
的坐标.
(3)在![]() 轴上有一动点
轴上有一动点![]() ,若
,若![]() ,试建立
,试建立![]() 关于
关于![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的运动范围;
的运动范围;
【答案】(1)y=![]() x2+1;M(0,2);(2)存在,Q(2
x2+1;M(0,2);(2)存在,Q(2![]() ,4)或(-2
,4)或(-2![]() ,4);(3)t=
,4);(3)t=![]() ,点P的运动范围为x轴上(
,点P的运动范围为x轴上(![]() ,0)及其左侧的部分
,0)及其左侧的部分
【解析】
(1)由抛物线的顶点坐标是(0,1),且过点(-2,2),故设其解析式为y=ax2+1,则利用待定系数法即可求得此抛物线的解析式,又由四边形OABC是平行四边形,则可求得点A与M的坐标;
(2)设△ABQ的边AB上的高为h,可得S△BCM=![]() BMOM=2,则又由S△ABQ=2S△BCM=
BMOM=2,则又由S△ABQ=2S△BCM=![]() AB×h,即可求得点Q的坐标;
AB×h,即可求得点Q的坐标;
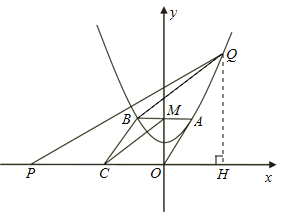
(3)作QH⊥x轴,交x轴于点H,即可证得△PQH∽△CMO,根据相似三角形的对应边成比例,即可求得x与t的关系式,求出t的取值范围,从而确定点P的运动范围.
解:(1)∵抛物线的顶点坐标是(0,1),且过点(-2,2),
故设其解析式为y=ax2+1,
则有:2=(-2)2×a+1,
得a=![]() ,
,
∴此抛物线的解析式为:y=![]() x2+1,
x2+1,
∵四边形OABC是平行四边形,
∴AB=OC=4,AB∥OC,
又∵y轴是抛物线的对称轴,
∴点A与B是抛物线上关于y轴的对称点,
则MA=MB=2,
即点A的横坐标是2,
则其纵坐标y=![]() ×22+1=2,
×22+1=2,
即点A(2,2),
故点M(0,2);
(2)设△ABQ的边AB上的高为h,
∵S△BCM=![]() BMOM=2,
BMOM=2,
∴S△ABQ=2S△BCM=![]() AB×h=4,
AB×h=4,
∴h=2,
∴点Q的纵坐标为4,代入y=![]() x2+1,
x2+1,
得x=±2![]() ,
,
∴存在符合条件的点Q,其坐标为(2![]() ,4),(-2/span>
,4),(-2/span>![]() ,4);
,4);
(3)作QH⊥x轴,交x轴于点H.
则∠QHP=∠MOC=90°,
∵PQ∥CM,
∴∠QPH=∠MCO,
∴△PQH∽△CMO,
∴![]() ,
,
即![]() ,
,
而y=![]() x2+1,
x2+1,
∴![]() ,
,
∴t=![]() ,
,
∴t的取值范围是:t≤![]() ,
,
∴点P的运动范围为x轴上(![]() ,0)及其左侧的部分.
,0)及其左侧的部分.


科目:初中数学 来源: 题型:
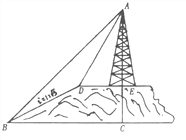
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
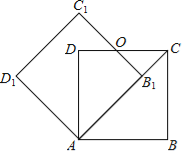
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米/秒的速度自A点出发沿AB方向运动,动点Q以2厘米/秒的速度自B点出发沿BC方向运动至C点停止,同时P点也停止运动若点P,Q同时出发运动了t秒,记△BPQ的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是( )
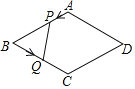
A.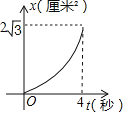 B.
B.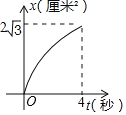
C.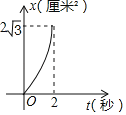 D.
D.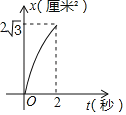
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
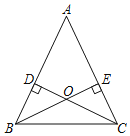
【题目】如图,锐角三角形ABC的两条高线BE、CD相交于点O,BE=CD.
(1)求证:BD=CE;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
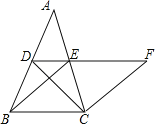
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
(1)求证:四边形BCFE是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
.
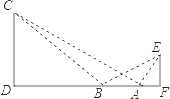
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
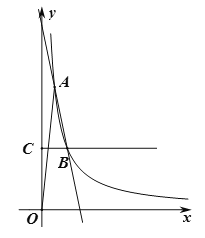
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于A,B两点,A点的坐标为
的图象在第一象限交于A,B两点,A点的坐标为![]() ,B点的坐标为
,B点的坐标为![]() ,连接
,连接![]() ,过B作
,过B作![]() 轴,垂足为C.
轴,垂足为C.
(1)求一次函数和反比例函数的表达式;
(2)在射线![]() 上是否存在一点D,使得
上是否存在一点D,使得![]() 是直角三角形,求出所有可能的D点坐标.
是直角三角形,求出所有可能的D点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com