
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于A,B两点,A点的坐标为
的图象在第一象限交于A,B两点,A点的坐标为![]() ,B点的坐标为
,B点的坐标为![]() ,连接
,连接![]() ,过B作
,过B作![]() 轴,垂足为C.
轴,垂足为C.
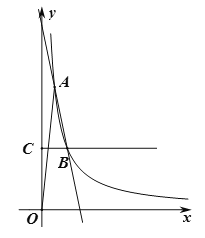
(1)求一次函数和反比例函数的表达式;
(2)在射线![]() 上是否存在一点D,使得
上是否存在一点D,使得![]() 是直角三角形,求出所有可能的D点坐标.
是直角三角形,求出所有可能的D点坐标.
【答案】(1)![]() ,y=
,y=![]() ;(2)(19,3)或(
;(2)(19,3)或(![]() ,3).
,3).
【解析】
(1)先利用待定系数法求出反比例函数解析式,进而确定出点A的坐标,再用待定系数法即可求出一次函数解析式;
(2)由于点D在射线CB上,所以∠AOD≠90°,当∠OAD=90°时,先求得直线AD的解析式,进而可求得点D坐标;当∠ODA=90°时,设AO、BC交于点F,如图2,则易知DF=![]() ,求出点F的坐标和AO的长即可解决问题.
,求出点F的坐标和AO的长即可解决问题.
解:(1)∵点B(2,3)在反比例函数![]() 的图象上,∴a=2×3=6,
的图象上,∴a=2×3=6,
∴反比例函数的表达式为y=![]() ,
,
∵点A的纵坐标为6,点A在反比例函数y=![]() 图象上,∴A(1,6),
图象上,∴A(1,6),
把点A(1,6)、B(2,3)代入![]() 中,得:
中,得:![]() ,解得:
,解得:![]() ,
,
∴一次函数的表达式为![]() ;
;
(2)由于点D在射线CB上,所以∠AOD≠90°.
①当∠OAD=90°时,如图1,∵直线OA的解析式为:![]() ,∴设直线AD的解析式为
,∴设直线AD的解析式为![]() ,
,
把点A(1,6)代入,得![]() ,∴直线AD的解析式为
,∴直线AD的解析式为![]() ,
,
当y=3时,x=19,∴D(19,3);
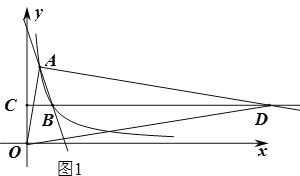
②当∠ODA=90°时,设AO、BC交于点F,如图2,
∵A(1,6),B(2,3),![]() 轴,
轴,
∴AF=OF=DF=![]() ,F(
,F(![]() ,3),
,3),
∴点D的坐标为(![]() ,3);
,3);
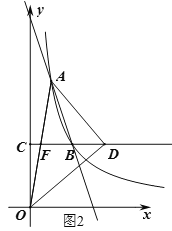
综上所述,满足条件的点D坐标为(19,3)或(![]() ,3).
,3).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一抛物线的顶点坐标是
中,一抛物线的顶点坐标是![]() ,且过点
,且过点![]() ,平行四边形
,平行四边形![]() 的顶点在
的顶点在![]() 此抛物线上,
此抛物线上,![]() 与
与![]() 轴相交于点
轴相交于点![]() .己知点
.己知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是抛物线上任意一点.
是抛物线上任意一点.
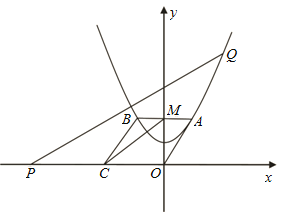
(1)求此抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在抛物线上是否存在点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍?若存在,求此时点
的面积的2倍?若存在,求此时点![]() 的坐标.
的坐标.
(3)在![]() 轴上有一动点
轴上有一动点![]() ,若
,若![]() ,试建立
,试建立![]() 关于
关于![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的运动范围;
的运动范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
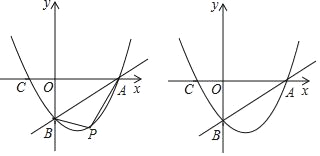
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
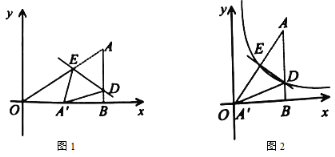
【题目】如图1,点A在第一象限,![]() 轴于B点,连结
轴于B点,连结![]() ,将
,将![]() 折叠,使
折叠,使![]() 点落在x轴上,折痕交
点落在x轴上,折痕交![]() 边于D点,交斜边
边于D点,交斜边![]() 于E点,(1)若A点的坐标为
于E点,(1)若A点的坐标为![]() ,当
,当![]() 时,点
时,点![]() 的坐标是______;(2)若
的坐标是______;(2)若![]() 与原点O重合,
与原点O重合,![]() ,双曲线
,双曲线![]() 的图象恰好经过D,E两点(如图2),则
的图象恰好经过D,E两点(如图2),则![]() ____.
____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+1)x+4k-3=0,当Rt△ABC的斜边a=![]() ,且两直角边b和c恰好是这个方程的两个根时,求△ABC的周长.
,且两直角边b和c恰好是这个方程的两个根时,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
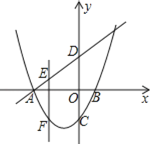
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“疾驰臭豆腐”是长沙知名地方小吃,某分店经理发现,当每份臭豆腐的售价为![]() 元时,每天能卖出
元时,每天能卖出![]() 份;当每份臭豆腐的售价每增加
份;当每份臭豆腐的售价每增加![]() 元时,每天就会少卖出
元时,每天就会少卖出![]() 份,设每份臭豆腐的售价增加
份,设每份臭豆腐的售价增加![]() 元时,一天的营业额为
元时,一天的营业额为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出
的函数关系式(不要求写出![]() 的取值范围);
的取值范围);
(2)考虑到顾客可接受价格![]() 元
元![]() 份的范围是
份的范围是![]() ,且
,且![]() 为整数,不考虑其他因素,则该分店的臭豆腐每份多少元时,每天的臭豆腐营业额最大?最大营业额是多少元?
为整数,不考虑其他因素,则该分店的臭豆腐每份多少元时,每天的臭豆腐营业额最大?最大营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
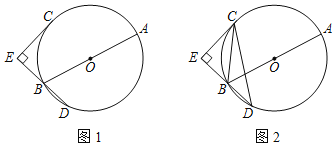
【题目】已知:AB为⊙O的直径,C、D为心⊙O上的点,C是优弧AD的中点,CE⊥DB交DB的延长线于点E.
(1)如图1,判断直线CE与⊙O的位置关系,并说明理由.
(2)如图2,若tan∠BCE=![]() ,连BC、CD,求cos∠BCD的值.
,连BC、CD,求cos∠BCD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com