
����Ŀ���Ӽص��ҵ���A��B��C������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
��������ʱ ��������ʱ��Ƶ�� ��· |
|
|
|
| �ϼ� |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
��߷��ڼ䣬����_________������A������B������C������·�ϵĹ��������Ӽص��ҵ�����ʱ������45�������Ŀ��������
 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳���4���ף���B��60�㣬����P��1����/����ٶ���A�������AB�����˶�������Q��2����/����ٶ���B�������BC�����˶���C��ֹͣ��ͬʱP��Ҳֹͣ�˶�����P��Qͬʱ�����˶���t�룬�ǡ�BPQ�����ΪS����2������ͼ�����ܱ�ʾS��t֮��ĺ�����ϵ���ǣ�������
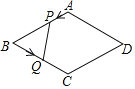
A.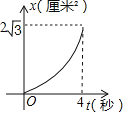 B.
B.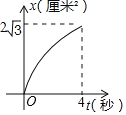
C.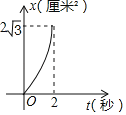 D.
D.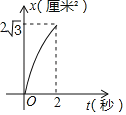
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijѧ�������EF��ʵ��¥CD֮���A������á�EAF=60����Ȼ�������ƶ�10��B������á�EBF=30������CBD=45����tan��CAD= ![]() ��
��
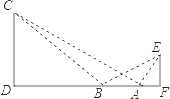
��1�������EF�ĸߣ�����������ţ���
��2�������EF��ʵ��¥CD֮���ˮƽ����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A����2����2����B��0��3����C��3��3����D��4����2����y�ǹ���x�Ķ��κ�����������y1������A��B��C��������y2������B��C��D��������y3������A��B��D��������y4������A��C��D�������жϣ�
�����������ߵĿ��ڷ�������£�
����x��0ʱ��������һ�������߱���ʽ�е�y����x���������С��
��������y1�Ķ�����������y2������Ϸ���
��������y4��y��Ľ����ڵ�B���Ϸ���
������ȷ���۵����Ϊ_____��
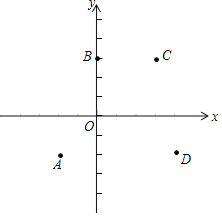
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
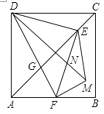
����Ŀ����ͼ�������� ABCD �У�AD��6���� E �ǶԽ��� AC ��һ�㣬���� DE������ E �� EF�� ED���� AB �ڵ� F������ DF���� AC �ڵ� G������EFG �� EF ���ۣ��õ���EFM������DM���� EF �ڵ� N������ F �� AB �ߵ��е㣬�� ��EDM �������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����A��1��2����
��1����b��1��c����4ʱ����ö��κ����ı���ʽ��
��2����֪��M��t��1��5����N��t+1��5���ڸö��κ�����ͼ���ϣ���ֱ��д��t��ȡֵ��Χ��
��3����a��1ʱ�����ö��κ�����ͼ����ֱ��y��3x��1���ڵ�P��Q��������������ֱ��PQ�·��IJ���ͼ���ΪC��
�����жϴ������ߵĶ����Ƿ�һ����ͼ��C�ϣ����ǣ���֤���������ǣ���ٷ�����
����֪��P���������߶Գ���ĶԳƵ�ΪP������P����ͼ��C�ϣ���b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�һ������A��B���㣬A�������Ϊ
��ͼ���ڵ�һ������A��B���㣬A�������Ϊ![]() ��B�������Ϊ
��B�������Ϊ![]() ������
������![]() ����B��
����B��![]() �ᣬ����ΪC��
�ᣬ����ΪC��
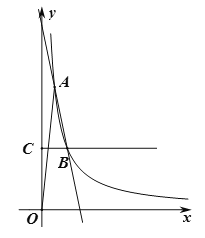
��1����һ�κ����ͷ����������ı���ʽ��
��2��������![]() ���Ƿ����һ��D��ʹ��
���Ƿ����һ��D��ʹ��![]() ��ֱ�������Σ�������п��ܵ�D�����꣮
��ֱ�������Σ�������п��ܵ�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��![]() ��x�ύ��A��C��A��C����ࣩ����B���������ϣ��������Ϊ1������BC��BO����FΪOB�е㣮
��x�ύ��A��C��A��C����ࣩ����B���������ϣ��������Ϊ1������BC��BO����FΪOB�е㣮
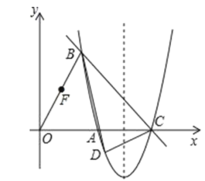
��1����ֱ��BC�ĺ�������ʽ��
��2������DΪ�����ߵ��������ϵ�һ�����㣬����BD��CD����EΪx����һ���㣬����BCD����������ʱ�����D�����꣬��|FE��DE|�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y��a��x��![]() ����x+
����x+![]() ����x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��DE�������ߵĶԳ��ᣬ��D��x���ϣ���E���������ϣ�ֱ��y��kx+
����x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��DE�������ߵĶԳ��ᣬ��D��x���ϣ���E���������ϣ�ֱ��y��kx+![]() ����A��C��
����A��C��
��1���������ߵĽ���ʽ��
��2����P�ǵڶ����Գ��������������һ�㣬����P��PQ��AC���Գ����ڵ�Q�����P�ĺ�����Ϊt���߶�QD�ij�Ϊd����d��t�ĺ�������ʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�ֱ��AC��Գ��ύ�ڵ�F����M�ڶԳ���ED�ϣ�����AM��AE����AMD��2��EAM������A��AG��AM������Dƽ����AE��ֱ���ڵ�G����N���߶�BP�ӳ�����һ�㣬����AN��MN��NF�����ı���NMGA���ı���NFDA�������ȣ���FN��AM�����P�����꣮
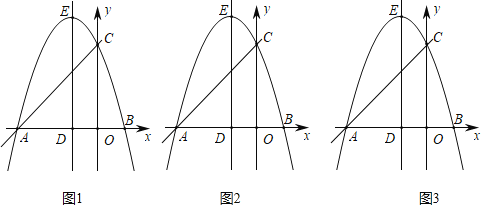
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com