
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=a(x﹣![]() )(x+
)(x+![]() )与x轴交于A、B两点,与y轴交于点C,直线DE是抛物线的对称轴,点D在x轴上,点E在抛物线上,直线y=kx+
)与x轴交于A、B两点,与y轴交于点C,直线DE是抛物线的对称轴,点D在x轴上,点E在抛物线上,直线y=kx+![]() 过点A、C.
过点A、C.
(1)求抛物线的解析式;
(2)点P是第二象限对称轴左侧抛物线上一点,过点P作PQ∥AC交对称轴于点Q,设点P的横坐标为t,线段QD的长为d,求d与t的函数解析式(不要求写出自变量t的取值范围);
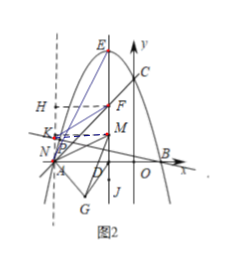
(3)在(2)的条件下,直线AC与对称轴交于点F,点M在对称轴ED上,连接AM、AE,∠AMD=2∠EAM,过点A作AG⊥AM交过点D平行于AE的直线于点G,点N是线段BP延长线上一点,连接AN、MN、NF,若四边形NMGA与四边形NFDA的面积相等,且FN∥AM,求点P的坐标.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ;(2)d=﹣
;(2)d=﹣![]() t2﹣
t2﹣![]() t+5;(3)P(﹣5,
t+5;(3)P(﹣5,![]() ).
).
【解析】
(1)由已知可求C(0,![]() ),再将点C代入抛物线解析式即可求出a的值,即可得到二次函数的解析式;
),再将点C代入抛物线解析式即可求出a的值,即可得到二次函数的解析式;
(2)P(t,﹣![]() t2﹣
t2﹣![]() t+
t+![]() ),过点P作PT⊥x轴,PS⊥y轴交DE于点L,则PT=﹣
),过点P作PT⊥x轴,PS⊥y轴交DE于点L,则PT=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ,PS=﹣t,在矩形PTOS和矩形PTDL中,有DT=PL=﹣t﹣
,PS=﹣t,在矩形PTOS和矩形PTDL中,有DT=PL=﹣t﹣![]() ,设AC交DE于点F,由∠PQL=∠AFL=∠ACO,则tan∠PQL=tan∠AFL=tan∠ACO=
,设AC交DE于点F,由∠PQL=∠AFL=∠ACO,则tan∠PQL=tan∠AFL=tan∠ACO=![]() ,QL=﹣
,QL=﹣![]() t﹣
t﹣![]() ,即可得到d=﹣
,即可得到d=﹣![]() t2﹣
t2﹣![]() t+5;
t+5;
(3)先证明△AMG≌△DFA,得到△AMN与△ANF的面积相等,过点M作MK⊥AN于点K,过点F作FH⊥AN于点H,再证明四边形HKMF为平行四边形,四边形AMFN为平行四边形,求出BN的解析式为y=﹣![]() x+
x+![]() ,即可求P点坐标.
,即可求P点坐标.
(1)∵直线y=kx+![]() 与y轴交于点C,
与y轴交于点C,
∴C(0,![]() ),
),
∴OC=![]() ,
,
∵y=a(x﹣![]() )(x+
)(x+![]() )经过点C,
)经过点C,
∴a=﹣![]() ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ;
;
(2)∵y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
∴设P(t,﹣![]() t2﹣
t2﹣![]() t+
t+![]() ),A(﹣
),A(﹣![]() ,0),B(
,0),B(![]() ,0),
,0),
∴tan∠ACO=![]() =
=![]() ,
,
过点P作PT⊥x轴,PS⊥y轴交DE于点L,
∴PT=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ,PS=﹣t,
,PS=﹣t,
∵DE是抛物线的对称轴,
∴D(﹣![]() ,0),
,0),
在矩形PTOS和矩形PTDL中,有DT=PL=﹣t﹣![]() ,
,
设AC交DE于点F,
∵PQ∥AC,DE∥y轴,
∴∠PQL=∠AFL=∠ACO,
∴tan∠PQL=tan∠AFL=tan∠ACO=![]() ,
,
∴QL=﹣![]() t﹣
t﹣![]() ,
,
∵DQ=DL+QL,
∴d=﹣![]() t2﹣
t2﹣![]() t+5;
t+5;
(3)∠EAM=α,则∠AMD=2∠EAM=2α,
∴∠AEM=∠EAM=α,
∴AM=EM,
∵DE=8,AD=4,
∴在RtADM中,AM2=(8-AM)2+42,
∴AM=EM=5,DM=3,
∵DG∥AE,
∴∠GDJ=∠AEM=α,
∴∠ADG=90°﹣α,
∵AM⊥AG,
∴∠MAG=90°,
∴∠DAG+∠MAD=∠AMD+∠MAD,
∴∠DAG=∠AMD=2α,
∴∠AGD=∠ADG=90°﹣α,
∴AG=AD=4,
∵tan∠AFD=![]() ,
,
∴DF=5,
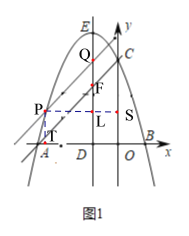
在△AMG与△DFA中,
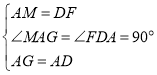 ,
,
∴△AMG≌△DFA(SAS),
∴△AMG与△DAF的面积相等,
∵四边形NMGA与四边形NFDA的面积相等,
∴△AMN与△ANF的面积相等,
如图2,过点M作MK⊥AN于点K,过点F作FH⊥AN于点H,
∴MK=FH,
∵MK∥FH,
∴四边形HKMF为平行四边形,
∴AN∥DE,
∴点N与点A的横坐标相等,
∵AM∥NF,
∴四边形AMFN为平行四边形,
∴AN=MF=DF﹣DM=2,
∴N(﹣![]() ,2),
,2),
∴BN的解析式为:y=﹣![]() x+
x+![]() ,
,
∴﹣![]() x+
x+![]() =﹣
=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
∴x=﹣5或x=![]() (舍),
(舍),
∴P(﹣5,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“疾驰臭豆腐”是长沙知名地方小吃,某分店经理发现,当每份臭豆腐的售价为![]() 元时,每天能卖出
元时,每天能卖出![]() 份;当每份臭豆腐的售价每增加
份;当每份臭豆腐的售价每增加![]() 元时,每天就会少卖出
元时,每天就会少卖出![]() 份,设每份臭豆腐的售价增加
份,设每份臭豆腐的售价增加![]() 元时,一天的营业额为
元时,一天的营业额为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出
的函数关系式(不要求写出![]() 的取值范围);
的取值范围);
(2)考虑到顾客可接受价格![]() 元
元![]() 份的范围是
份的范围是![]() ,且
,且![]() 为整数,不考虑其他因素,则该分店的臭豆腐每份多少元时,每天的臭豆腐营业额最大?最大营业额是多少元?
为整数,不考虑其他因素,则该分店的臭豆腐每份多少元时,每天的臭豆腐营业额最大?最大营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉善县将开展以“珍爱生命,铁拳护航”为主题的交通知识竞赛,某校对参加选拔赛的若干名同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
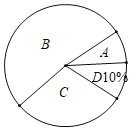
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)“A等级”的4名同学中有3名男生和1名女生,现从中随机挑选2名同学代表学校参加全县比赛,请用树状图法或列表法求出恰好选中“一男一女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车与乙车同时从A地出发去往B地,如图所示,折线O﹣A﹣B﹣C和射线OC分别是甲、乙两车行进过程中路程与时间的关系,已知甲车中途有事停留36分钟后再继续前往C地,两车同时到达C地,则下列说法:①乙车的速度为70千米/时;②甲车再次出发后的速度为100千米/时;③两车在到达B地前不会相遇;④甲车再次出发时,两车相距60千米.其中正确的有( )
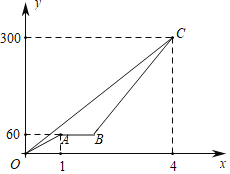
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣3,2),B(0,1),将线段AB沿x轴的正方向平移n(n>0)个单位,得到线段A′,B′恰好都落在反比例函数y![]() (m≠0)的图象上.
(m≠0)的图象上.
(1)用含n的代数式表示点A′,B′的坐标;
(2)求n的值和反比例函数y![]() (m≠0)的表达式;
(m≠0)的表达式;
(3)点C为反比例函数y![]() (m≠0)图象上的一个动点,直线CA′与x轴交于点D,若CD=2A′D,请直接写出点C的坐标.
(m≠0)图象上的一个动点,直线CA′与x轴交于点D,若CD=2A′D,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
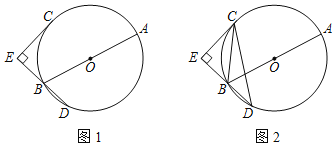
【题目】已知:AB为⊙O的直径,C、D为心⊙O上的点,C是优弧AD的中点,CE⊥DB交DB的延长线于点E.
(1)如图1,判断直线CE与⊙O的位置关系,并说明理由.
(2)如图2,若tan∠BCE=![]() ,连BC、CD,求cos∠BCD的值.
,连BC、CD,求cos∠BCD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,填空:当点
,填空:当点![]() 位于__________时,线段
位于__________时,线段![]() 的长取到最大值__________,且最大值为;(用含
的长取到最大值__________,且最大值为;(用含![]() 、
、![]() 的式子表示).
的式子表示).

(2)如图2,若点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为边,作等边
为边,作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .
.

①图中与线段![]() 相等的线段是线段__________,并说明理由;
相等的线段是线段__________,并说明理由;
②直接写出线段![]() 长的最大值为__________.
长的最大值为__________.
(3)如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 长的最大值为__________,及此时点
长的最大值为__________,及此时点![]() 的坐标为__________.(提示:等腰直角三角形的三边长
的坐标为__________.(提示:等腰直角三角形的三边长![]() 、
、![]() 、
、![]() 满足
满足![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交L于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交L于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2019等于_____.
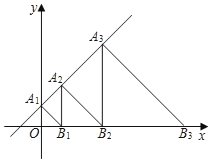
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com