
【题目】写出下列命题的已知、求证,并完成证明过程.
(1)命题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边”).
已知:如图, .
求证: .
(2)证明命题
【答案】
(1)在△ABC中,∠B=∠C;AB=AC
(2)
证明:过点A作AD⊥BC于D,
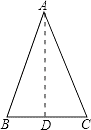
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
![]()
∴△ABD≌△ACD(AAS),
∴AB=AC.
【解析】解:在△ABC中,∠B=∠C,AB=AC,
根据图示,分析原命题,找出其条件与结论,然后根据∠B=∠C证明△ABC为等腰三角形,从而得出结论.
【考点精析】通过灵活运用等腰三角形的性质和命题与定理,掌握等腰三角形的两个底角相等(简称:等边对等角);我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):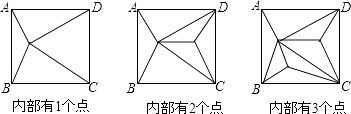
(1)填写如表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 ![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( ) 
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF. 
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC; ②若半圆O的半径为12,求阴影部分的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com