
����Ŀ����ͼ��������ABCD�ڲ������ɸ��㣬����Щ���Լ�������ABCD�Ķ���A��B��C��D��ԭ�����ηָ��һЩ�����Σ�����ص�����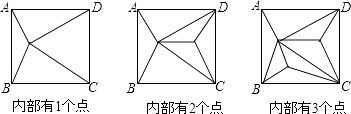
��1��������
������ABCD�ڵ�ĸ��� | 1 | 2 | 3 | 4 | �� | n |
�ָ�ɵ������εĸ��� | 4 | 6 | �� |
��2�����ԭ�����α��ָ��2016�������Σ���ʱ������ABCD�ڲ��ж��ٸ��㣿
��3�����������£����������ָܷ��2017�������Σ����ܣ���ʱ������ABCD�ڲ��ж��ٸ��㣿�����ܣ���˵�����ɣ�
��4�����Ͻ��ۣ�����ʲô���֣���д��һ�����ɣ�
���𰸡�
��1��8��10��2��n+1��
��2��
�⣺�����Ϊn��
��2��n+1��=2016��
���n=1007��
��ԭ�����α��ָ��2016��������ʱ������ABCD�ڲ���1007���㣮
��3��
�⣺�����Ϊn��
��2��n+1��=2017��
���n=1007.5��
��ԭ�����β����ָ��2017�������Σ�
��4��
�⣺���ָ�ɵ������εĸ�����Զ��ż������
����������1������ͼ���ص��ҳ�������ABCD�ڵ�ĸ�����ָ�ɵ������εĸ����Ĺ�ϵ���ܽ���ɼ��ɣ���2�����ݹ����г����̣��ⷽ�̵õ��𰸣���3���г����������������У������У���4���������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=x2��2x+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0����3����[ͼ2��ͼ3Ϊ�����ͼ]
��1��k= �� ��A������Ϊ �� ��B������Ϊ��
��2����������y=x2��2x+k�Ķ���ΪM�����ı���ABMC�������
��3����x���·������������Ƿ����һ��D��ʹ�ı���ABDC�������������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
��4����������y=x2��2x+k�����Q��ʹ��BCQ����BCΪֱ�DZߵ�ֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������ABCD�У�AD��BC��AD=1��BC=3��AB=CD=2����E��BC���ϣ�AE��BD���ڵ�F����BAE=��DBC�� 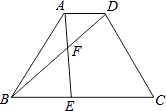
��1����֤����ABE�ס�BCD��
��2����tan��DBC��ֵ��
��3�����߶�BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д�������������֪����֤�������֤�����̣�
��1�����⣺���һ�������ε���������ȣ���ô�����������Եı�Ҳ��ȣ���ƣ����ȽǶԵȱߡ�����
��֪����ͼ�� ��
��֤�� ��
��2��֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ż������ķ�չ���������������������ǵ������ͼ��ʾ���ǡ��ε�˳�糵���롰�εο쳵������ʻ���x�������Ʒ�y��Ԫ��֮��ĺ�����ϵͼ��������˵����������ȷ˵���ĸ����У� �� �١��쳵����ʻ��̲�����5����Ʒ�8Ԫ��
�ڡ�˳�糵����ʻ��̳���2����IJ��֣�ÿ����Ʒ�1.2Ԫ��
��A���������6.5��10.4����
�ܴӺϷ���վ����չ���ĵ������15�����˳�糵��Ҫ�ȡ��쳵������3.4Ԫ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Զ��С��ͬѧ�����п���ѡ����Ŀ֮һ��ij���������ϣ�������ʦ��¼��С�յ�һ��������Զѵ���ɼ����±���
�ɼ���m�� | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
���� | 1 | 1 | 2 | 5 | 1 |
�����й����������ݵ�˵������ȷ���ǣ� ��
A.������2.45
B.ƽ������2.45
C.�����2.5
D.������0.48
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������C�ڡ�O�ϣ���P��ֱ��AB�ϵ�һ�㣨����A�غϣ�������P��AB�Ĵ��߽�BC�ڵ�Q�� 
��1�����߶�PQ��ȡһ��D��ʹDQ=DC������DC�����ж�CD���O��λ�ù�ϵ����˵�����ɣ�
��2����cosB= ![]() ��BP=6��AP=1����QC�ij���
��BP=6��AP=1����QC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��������У� �� ������֮���߶���̣��ڵ��ǵ����߾�����ȵĵ��ڽǵ�ƽ�����ϣ�
�۹�һ������ֻ��һ��ֱ������ֱ֪��ƽ�У��ܴ�ֱ��ͬһֱ�ߵ�����ֱ��ƽ�У�
������O����AB��CD���ڵ�P����PAPB=PCPD��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾABΪ��O��һ���ң���CΪ�ӻ�AB���е㣬EΪ�Ż�AB��һ�㣬��F��AE���ӳ����ϣ���BE=EF���߶�CE����AB�ڵ�D��
����֤��CE��BF��
����BD=2����EA��EB��EC=3��1�� ![]() �����BCD�������ע������Բ�ĶԳ��Կ�֪OC��AB����
�����BCD�������ע������Բ�ĶԳ��Կ�֪OC��AB����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com