Question

2．据气象台预报，一强台风的中心位于舟山城区东南方向（36$\sqrt{6}$+108$\sqrt{2}$）千米的海面上，目前台风中心正以20千米/时的速度向北偏西60°的方向移动，距台风中心50千米的圆形区域均会受到强台风袭击，已知象山位于舟山正南方向72千米处，宁波位于象山北偏西30°的60千米处．请问：
（1）台风中心是否经过象山？
（2）舟山、宁波是否会受这次强台风的袭击？如果会，请计算处受强台风袭击的时间，如果不会，请说明理由．

Answer 1

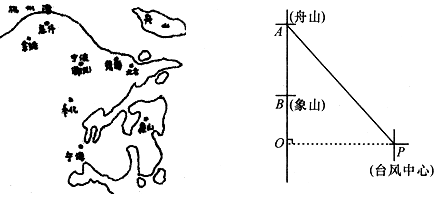
分析 （1）如图1，延长台风中心移动射线PQ与AO相交于M，解直角三角形得到MO=OPtan30°=（36$\sqrt{3}$+108）•$\frac{\sqrt{3}}{3}$=36+36$\sqrt{3}$=OB，于是得到结论；
（2）如图2，C为宁波，过作CN⊥PB于N，AD⊥PB于D，由题意可得∠CBN=30°，求得C到PB的距离CN=60sin30°=30，于是得到宁波会受到此次台风强袭击；由于50km为半径的圆与PB相交的弦长等于2$\sqrt{5{0}^{2}-3{0}^{2}}$=40，于是得到受袭击时间；解直角三角形得到A到PQ的距离AD=AB•sin60°=72×$\frac{\sqrt{3}}{2}$=36$\sqrt{3}$，于是得到结论．

解答 解：（1）如图1，延长台风中心移动射线PQ与AO相交于M
∵AP=36$\sqrt{6}$+108$\sqrt{2}$，∠OAP=∠APO=45°，AO⊥OP，
∴AO=OP=36$\sqrt{3}$+108，BO=AO-AB=36$\sqrt{3}$+36，
∵∠OPM=30°，
∴MO=OPtan30°=（36$\sqrt{3}$+108）•$\frac{\sqrt{3}}{3}$=36+36$\sqrt{3}$=OB，
∴M与B重合，
∴台风中心必经过象山；

（2）如图2，C为宁波，过作CN⊥PB于N，AD⊥PB于D，
由题意可得∠CBN=30°，C到PB的距离CN=60sin30°=30，
∴宁波会受到此次台风强袭击；
∵50km为半径的圆与PB相交的弦长等于2$\sqrt{5{0}^{2}-3{0}^{2}}$=40，
∴受袭击时间2（时），
∵A到PQ的距离AD=AB•sin60°=72×$\frac{\sqrt{3}}{2}$=36$\sqrt{3}$，
∴舟山不会遭受此次台风的强袭击，
综上所述：舟山不会遭受此次台风的强袭击；宁波：会，受袭击时间为2时．

点评 本题考查解直角三角形的应用，有一定的难度，解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．