
分析 观察所求式子可知,直接进行线段比值推导明显很复杂,因此可考虑从面积的角度入手.不妨设S△ABD=S1,S△BDC=S2,SADC=S3,则$\frac{AD}{DE}$、$\frac{BD}{DF}$、$\frac{CD}{DP}$均可以用S1、S2、S3表示,三者相乘化简即可得结果.
解答 解:设S△ABD=S1,S△BDC=S2,SADC=S3,
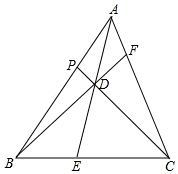
则$\frac{AD}{DE}=\frac{{S}_{ABD}}{{S}_{BDE}}$=$\frac{{S}_{△ADC}}{{S}_{△DEC}}$=$\frac{{S}_{△ABD}+{S}_{△ADC}}{{S}_{△BDE}+{S}_{△DEC}}$=$\frac{{S}_{1}+{S}_{3}}{{S}_{2}}$,
同理:$\frac{BD}{DF}$=$\frac{{S}_{1}+{S}_{2}}{{S}_{3}}$,$\frac{CD}{DP}=\frac{{S}_{2}+{S}_{S}}{{S}_{1}}$,
$\frac{AD}{DE}+\frac{BD}{DF}+\frac{CD}{DP}$=$\frac{{S}_{1}+{S}_{3}}{{S}_{2}}$+$\frac{{S}_{1}+{S}_{2}}{{S}_{3}}$+$\frac{{S}_{2}+{S}_{S}}{{S}_{1}}$=1994,
$\frac{AD}{DE}•\frac{BD}{DF}•\frac{CD}{DP}$=$\frac{{S}_{1}+{S}_{3}}{{S}_{2}}$•$\frac{{S}_{1}+{S}_{2}}{{S}_{3}}$•$\frac{{S}_{2}+{S}_{S}}{{S}_{1}}$=1994+2=1996.
点评 本题考查相似三角形的判定与性质及面积法,难度较大.在面对较复杂的线段比例问题时,借助面积法往往会使问题得以简化,这一点值得注意.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 身高180cm和身高90cm | B. | 向东走5公里和向南走5公里 | ||
| C. | 收入300元和支出300元 | D. | 使用汽油10公斤和浪费酒精10公斤 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 其图象的开口向下 | B. | 其图象的对称轴为x=-3 | ||
| C. | 其最大值为1 | D. | 当x<3时,y随x的增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com