
 正方形ABCD,∠DEA=15°.ED=EC,求证:△DEC为等边三角形.
正方形ABCD,∠DEA=15°.ED=EC,求证:△DEC为等边三角形. 分析 利用反证法证明,①假设DE=EC>CD,推出矛盾;②假设DE=EC<DC,推出矛盾即可.
解答 证明:如图,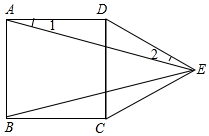 设∠EDC=∠ECD=α,则∠DEC=180°-2α
设∠EDC=∠ECD=α,则∠DEC=180°-2α
假设DE=EC>CD,
则有α>180-2α,
∴α>60°,
∵∠ADC=90°,
∴∠ADE>150°,∵∠2=15°,
∴∠1<15°,
∴∠1<∠2,
∴DE<AD,即DE<CD与假设矛盾,
∴假设不成立.
假设DE=EC<DC,
则有α<180°-2α,
∴α<60°,
∴∠ADE<150°,∵∠2=15°,
∴∠1>15°,
∴∠1>∠2,
∴DE>AD即DE>CD,与假设矛盾,
∴假设不成立,
∴DE=EC=DC,
∴△DEC是等边三角形.
点评 本题考查正方形的性质、等边三角形的判定、反证法等知识,解题的关键是掌握反证法的步骤,属于中考常考题型.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{6}$$÷\sqrt{2}$=$\sqrt{3}$ | D. | ($\sqrt{2}$+1)($\sqrt{2}$-1)=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=8,BC=10,AC=6,动点P从点C出发,沿着CB运动,速度为每秒2个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
在△ABC中,AB=8,BC=10,AC=6,动点P从点C出发,沿着CB运动,速度为每秒2个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com