Question

【题目】如图，在等腰梯形ABCD中，AD∥BC，AD=3cm，BC=7cm，∠B=60°,P为下底BC边上一点（不与B、C重合），连结AP，过P点作PE交DC于E，使得∠APE=∠B.

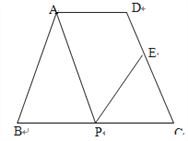
(1)求证：△ABP∽△PCE；

(2)求腰AB的长；

(3)在底边BC上是否存在一点P，使得DE:EC=5:3.如果存在，求出BP的长；如果不存在，请说明理由。

Answer 1

【答案】（2）4cm（3）BP=1cm或BP=6cm

【解析】试题分析：（1）欲证△ABP∽△PCE，需找出两组对应角相等；由等腰梯形的性质可得出∠B=∠C，根据三角形外角的性质可证得∠EPC=∠BAP；由此得证；

（2）可过作AF⊥BC于F，由等腰梯形的性质得到AF是BC、AD差的一半，在Rt△ABF中，根据∠B的度数及BF的长即可求得AB的值；

（3）在（2）中求得了AB的长，即可求出DE：EC=5：3时，DE、CE的值．设BP的长为x，进而可表示出PC的长，然后根据（1）的相似三角形，可得出关于AB、BP、PC、CE的比例关系式，由此可得出关于x的分式方程，若方程有解，则x的值即为BP的长．若方程无解，则说明不存在符合条件的P点．

试题解析：证明：（1）∠BAP+∠BPA=120°

∠APB+∠CPE=120°

∴∠BAP=∠CPE

又∠ABP=∠PCE

∴△ABP∽△PCE

（2）过A、D分别作AG⊥BC，DH⊥BC

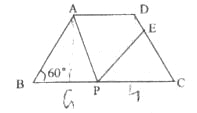
易得四边形AGHD是矩形

GH=AD=3cm

∴cm

在Rt△ABG中

cm

（3）由DE:EC=5：3

∴, .

又△ABP∽△PCE

∴

即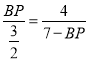

BP(7-BP)=6

BP=1cm或BP=6cm