
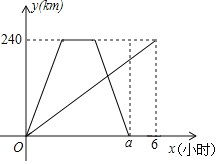
����Ŀ��A��B�������240km������Ħ�г���A��ʻ��B�أ��Ҽ�ʻ������B��ʻ��A�أ���������ͬʱ�������ҴﵽA��ͣ��1Сʱ��ԭ·ԭ�ٷ���B�أ��ױ�����1Сʱ����B�أ��ס���������ʻ�����о�������ʻ��������������Գ������·��y��km����������ʱ��x��h���Ĺ�ϵ��ͼ�����ͼ��ش��������⣮
��1���������仯�����У��Ա�����______���������______��
��2��a��ֵΪ______��
��3������B�ع���______Сʱ������Ħ�г����ٶ���______km/h��
��4���Ҽ�ʻ�������ٶ��Ƕ���km/h��
���𰸡���1�������õ�ʱ��x��h����������������Գ������·��y��km����2��5��3��6��4��![]() km/h
km/h
��������
��1�����ݺ���ͼ��ͺ����еĸ����ɣ�
��2�����üױ�����1Сʱ����B�صó�a��ֵ���ɣ�
��3������ͼ��ó�����B�ص�ʱ����ٶȼ��ɣ�
��4�����ú���ͼ��ó��Ҽ�ʻ������ʱ�䣬�����ó��ٶȣ�
��1���Ա����������õ�ʱ��x��h����������Ǽ�����������Գ������·��y��km����
�ʴ�Ϊ�������õ�ʱ��x��h����������������Գ������·��y��km����
��2����Ϊ�ױ�����1Сʱ����B�أ�����a=6-1=5��
�ʴ�Ϊ��5��
��3������B�ع���6Сʱ������Ħ�г����ٶ���![]() km/h��
km/h��
�ʴ�Ϊ��6��40��
��4���������֪���Ҽ�ʻ������ʻ��ʱ��Ϊ5-1=4��h����
�Ҽ�ʻ�������ٶ��ǣ�![]() ��km/h����
��km/h����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������й�����˾�ƻ�����A�ͺ�B�����ֻ������ܹ�������10����������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ��
��1������A�ͺ�B������ÿ�����������Ԫ��
��2��Ԥ����ij��·��A�ͺ�B������ÿ������ؿ����ֱ�Ϊ60���˴κ�100���˴Σ����ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ���ù�˾���ļ��ֹ���������
��3���ڣ�2���������£����ֹ��������ܷ������٣������ܷ����Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCΪ����ֱ�������Σ�AB=AC����ADEΪ����ֱ�������Σ�AD=AE����D��ֱ��BC�ϣ�����CE��
��1���жϣ���CE��CD��BC֮���������ϵ����CE��BC����ֱ��֮���λ�ù�ϵ����˵�����ɣ�
��2����D��CB�ӳ����ϣ���1���еĽ����Ƿ����������������ֱ��д�����ۣ�������������˵�����ɣ�
��3����D��BC�ӳ����ϣ���1���еĽ����Ƿ����������������ֱ��д�����ۣ�������������д���㷢�ֵĽ��ۣ������㣺��CE=10cm��CD=2cmʱ��BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��x2+bx+c������B����1��0���͵�C��2��3����
��1����������ߵĺ�������ʽ��
��2�����������������ƽ�ƺ���㣨��2����1������ȷ��ƽ�Ƶķ����ƽ�Ƶľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AF��CD��CBƽ�֡�ACD��BDƽ�֡�EBF����BC��BD�����н��ۣ��� BCƽ�֡�ABE���� AC��BE���� ��CBE+��D��90�㣻�� ��DEB��2��ABC��������ȷ���۵ĸ����У�������

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ֽƬABC�У�AD��BC���D��BC=2��AD=![]() ����AD�������������Σ���������������ƴ��ƽ���ı��Σ���ƽ���ı����нϳ��Խ��ߵij�Ϊ__________��
����AD�������������Σ���������������ƴ��ƽ���ı��Σ���ƽ���ı����нϳ��Խ��ߵij�Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����x�ύ�ڵ�A,B����y�ύ�ڵ�C����P�Ǹú���ͼ���ϵĶ��㣬��λ�ڵ�һ���ޣ����P�ĺ�����Ϊx��
��ͼ����x�ύ�ڵ�A,B����y�ύ�ڵ�C����P�Ǹú���ͼ���ϵĶ��㣬��λ�ڵ�һ���ޣ����P�ĺ�����Ϊx��
��1��д���߶�AC, BC�ij��ȣ�AC= ��BC= ��
��2������BCP�����ΪS����S����x�ĺ�������ʽ��
��3������P��PH��BC������ΪH������AH,AP����AP��BC���ڵ�K��̽�����Ƿ�����ı���ACPHΪƽ���ı��Σ������ڣ������![]() ��ֵ���������ڣ���˵�����ɣ������
��ֵ���������ڣ���˵�����ɣ������![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У�������Ϊ�ж���ABD�ա�BAC�������ǣ� )

A. ��D����C����BAD����ABC B. ��BAD����ABC����ABD����BAC
C. BD��AC����BAD����ABC D. AD��BC��BD��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AC��BC��2����C��90������һ��������ǰ��ֱ�Ƕ������б��AB���е�P���������ǰ��Ƶ�P��ת�����ǰ����ֱ�DZ߷ֱ�����AC��CB��D��E���㣮��ͼ�١��ڡ�������ת���ǰ�õ���ͼ���е�3��������о���
��1�����ǰ��Ƶ�P��ת���۲��߶�PD��PE֮����ʲô������ϵ�������ͼ��˵�����ɣ�
��2�����ǰ��Ƶ�P��ת����PCE�Ƿ��ܳ�Ϊ���������Σ����ܣ�ָ�������������д����PCEΪ����������ʱBE�ij����������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com