
【题目】△ABC为等腰直角三角形,AB=AC,△ADE为等腰直角三角形,AD=AE,点D在直线BC上,连接CE.
(1)判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;
(2)若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;
(3)若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.

【答案】(1)①BC=CE+CD;②BC⊥CE,理由见解析;(2)CE⊥BC成立;BC=CD+CE不成立,结论:CD=CE+BC,理由见解析;(3)CE⊥BC成立;BC=CD+CE不成立,结论:CE=BC+CD, BC=8cm.
【解析】
(1)证明△DAB≌△EAC,即可得到BD=CE,∠B=∠ACE=45°,所以就有BC=BD+CD=CE+CD;又因∠BCE=∠ACB+∠ACE=90°,∠ABC=∠BCA=45°,得到BC⊥CF
(2)同样先证明出△DAB≌△EAC,得到BD=CE,∠ABD=∠ACE,有CD=BD+BC =CE+BC;又因∠ABD=∠ACE=180°-∠ABC=180°-45°=135°,得到∠BCE=∠ACE-∠ACB=135°-450=90°,即BC⊥CE;
(3)同样先证△DAB≌△EAC,得到BD=CE,∠ABD=∠ACE,有CE=BD=BC+CD,
又因CE=BC+CD,所以BC=CE-CD=10-2=8(cm).
(1)①BC=CE+CD;②BC⊥CE,
理由如下:∵△ABC和△ADE是等腰三角形,AB=ACAD=AE,
∵∠BAC=∠DAE=90°,∠ABC=∠BCA=45°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,
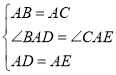 ,
,
∴△DAB≌△EAC(SAS),
∴BD=CE,∠B=∠ACE=45°,
∵BC=BD+CD,
∴BC=CE+CD,
∵∠BCE=∠ACB+∠ACE=90°,∠ABC=∠BCA=45°,
∴BC⊥CF;
(2)CE⊥BC成立;BC=CD+CE不成立,结论:CD=CE+BC,
理由如下:∵△ABC和△ADE是等腰三角形,AB=ACAD=AE,
∵∠BAC=∠DAE=90°,∠ABC=∠BCA=45°,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠BAD=∠CAE,
在△DAB与△EAC中,
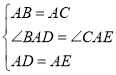 ,
,
∴△DAB≌△EAC(SAS),
∴BD=CE,∠ABD=∠ACE,
∵DC=BD+BC,
∴CD=CE+BC,
∵∠ABD=∠ACE=180°-∠ABC=180°-45°=135°,
∴∠BCE=∠ACE-∠ACB=135°-450=90°,
∴BC⊥CE;
(3)CE⊥BC成立;BC=CD+CE不成立,结论:CE=BC+CD,
同(1)可以得到△DAB≌△EAC,
∴BD=CE,∠ABD=∠ACE,
∴CE=BD=BC+CD,
∵CE=BC+CD, ∴BC=CE-CD=10-2=8(cm).


科目:初中数学 来源: 题型:
【题目】我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、字相乘法等等,将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫做分组分解.
例如:![]()
利用这种分组的思想方法解决下列问题:
(1)分解因式![]() ;
;
(2)![]() 三边a,b,c满足
三边a,b,c满足![]() 判断
判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
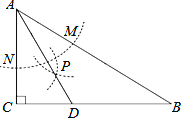
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB、AC于点M、N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,射线AP交边BC于点D.下列说法错误的是( )
MN的长为半径画弧,两弧交于点P,射线AP交边BC于点D.下列说法错误的是( )
A. ![]() B. 若
B. 若![]() ,则点D到AB的距离为2
,则点D到AB的距离为2
C. 若![]() ,则
,则![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上请完成下列各题
(1)随机抽取1张,求抽到卡片数字是奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?
(3)在(2)的条件下,试求组成的两位数是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠AEB=90°,点F是边AE上的一点,D是EF的中点,过点F作BE的平行线交BD的延长线于点C.若CF=AF,BE=6cm,DE=3cm,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示则这20户家庭该月用电量的众数和中位数、平均数分别是( )

A. 180,160,164B. 160,180;164C. 160,160,164D. 180,180,164
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
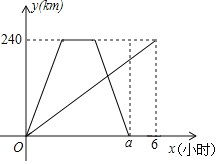
【题目】A、B两地相距240km,甲骑摩托车由A地驶往B地,乙驾驶汽车由B地驶往A地,甲乙两人同时出发,乙达到A地停留1小时后,按原路原速返回B地,甲比乙晚1小时到达B地,甲、乙两人行驶过程中均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.
(1)在上述变化过程中,自变量是______,因变量是______;
(2)a的值为______;
(3)甲到达B地共需______小时;甲骑摩托车的速度是______km/h;
(4)乙驾驶汽车的速度是多少km/h?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活与工作都离不开手机和电脑的今天,青少年近视、散光等眼问题日趋严重,为宣传2018全国爱眼日(6月6日),增强大众近视防控意识,某青少年视力矫正中心举办了主题为“永康降度还您一双明亮的眼睛”的降度明星大赛,现根据大赛公布的结果,将所有参赛孩子双眼降度之和(含近视和散光)情况绘制成了如下的统计表:
所降度数(度) | 100 | 200 | 300 | 400 | 500 | 600 |
人数(人) | 12 | 18 | 24 | 4 | 1 | 1 |
(1)求参加降度明星大赛的孩子共有多少人?
(2)求出所有参赛孩子所降度数的众数、中位数和平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com