
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() 且开口向下,则下列结论:①抛物线经过点
且开口向下,则下列结论:①抛物线经过点![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④对于任意实数
有两个不相等的实数根;④对于任意实数![]() ,
,![]() 总成立。其中结论正确的个数为( )
总成立。其中结论正确的个数为( )
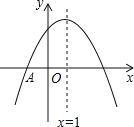
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
逐一分析4条结论是否正确:①根据抛物线的顶点坐标![]() ,得出对称轴为x=1,再根据抛物线的对称性得出①正确;②根据抛物线的对称轴为x=1,即可得出b+2a=0,再根据开口方向,即可得出②正确;③根据顶点坐标
,得出对称轴为x=1,再根据抛物线的对称性得出①正确;②根据抛物线的对称轴为x=1,即可得出b+2a=0,再根据开口方向,即可得出②正确;③根据顶点坐标![]() 且开口向下,得出直线
且开口向下,得出直线![]() 与抛物线
与抛物线![]() 没有交点,即可得出③错误;④抛物线开口向下,对称轴为x=1,有最大值
没有交点,即可得出③错误;④抛物线开口向下,对称轴为x=1,有最大值![]() ,再根据x=m时的函数值为
,再根据x=m时的函数值为![]() ,由此即可得出④错误,综上即可得出结论.
,由此即可得出④错误,综上即可得出结论.
解:①∵抛物线y=ax2+bx+c(a≠0)的顶点坐标![]()
∴对称轴为x=1,
∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴则![]() 关于对称轴x=1的对称点的坐标为
关于对称轴x=1的对称点的坐标为![]()
∴抛物线经过点![]() ;∴①正确
;∴①正确
②∵抛物线的对称轴为x=1,
∴-![]() =1,∴-2a=b,∴2a+b=0
=1,∴-2a=b,∴2a+b=0
∵开口向下,∴a![]()
∴![]() ;
;
∴②正确;
③∵![]()
∴![]()
∵顶点坐标![]() 且开口向下,
且开口向下,
∴直线![]() 与抛物线
与抛物线![]() 没有交点,
没有交点,
∴关于![]() 的方程
的方程![]() 没有实数根;
没有实数根;
∴③错误;
④∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,开口向下
∴当x=1,![]()
∵当x=t时,y= at2+bt+c
∵![]() 为任意实数
为任意实数
∴![]() ≤
≤![]()
∴![]() .
.
∴![]()
∴④错误.
故选:B.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )

A.①②④ B.③④ C.①③④ D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
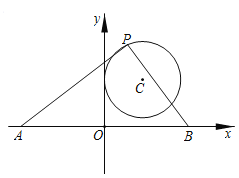
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
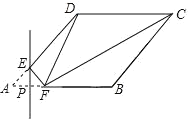
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com