练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解分式方程：（1）；

    （2）.

    【答案】（1）x=4；（2）无解

    【解析】

    （1）两边乘以最简公分母(x-2)转化为整式方程，然后求出整式方程的解，再代入最简公分母检验即可得出分式方程的解；

    （2）两边乘以最简公分母(x+1)(x-1)转化为整式方程，然后求出整式方程的解，再代入最简公分母检验即可得出分式方程的解.

    解：（1）方程的两边同乘(x-2)，得：1-x+2(x-2)=1，

    解得：x=4．

    检验：当x=4时，x-2=2≠0，

    所以x=4是原分式方程的解；

    （2）方程的两边同乘(x+1)(x-1)，得：(x+1)2-4=(x+1)(x-1)，

    解得：x=1.

    检验：当x=1时，(x+1)(x-1)=0，即x=1不是原分式方程的解.

    则原方程无解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，有下列四种结论：①AB＝AD；②∠B＝∠D；③∠BAC＝∠DAC；④BC＝DC.以其中的2个结论作为依据不能判定△ABC≌△ADC的是(　　)

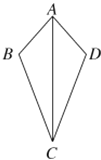
    A. ①② B. ①③ C. ①④ D. ②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和格点P．

    （1）以A点为位似中心，将△ABC在网格中放大成△AB1C1，使=2，请画出△AB1C1；

    （2）以P点为三角形的一个顶点，请画一个格点△PMN，使△PMN∽△ABC，且相似比为．

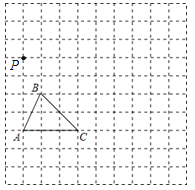
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，直线与轴交于点，交轴于点，直线与关于轴对称，交轴于点，

    （1）求直线的解析式；

    （2）过点在外作直线，过点作于点,过点作于点 ．求证：

    （3）如图2，如果沿轴向右平移，边交轴于点，点是的延长线上的一点，且，与轴交于点 ，在平移的过程中，的长度是否为定值，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2013年初开始实施后，实际每年绿化面积是原计划的1.6倍，这样可提前4年完成任务．

    （1）问实际每年绿化面积多少万平方米？

    （2）为加大创城力度，市政府决定从2016年起加快绿化速度，要求不超过2年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示，边长为a的正方形中有一个边长为b的小正方形，如图2所示是由图1中阴影部分拼成的一个正方形．

    （1）设图1中阴影部分面积为S1，图2中阴影部分面积为S2．请直接用含a，b的代数式表示S1，S2；

    （2）请写出上述过程所揭示的乘法公式；

    （3）试利用这个公式计算：（2+1）（22+1）（24+1）（28+1）+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某化工车间发生有害气体泄漏，从泄漏开始到完全控制利用了，之后将对泄漏的有害气体进行处理，线段表示气体泄漏时车间内检测表显示数据与时间() 之间的函数关系()， 反比例函数对应曲线表示气体泄漏控制后检测表显示数据与时间() 之间的函数关系().根据图像解答下列问题:

    (1)试求出检测表在气体泄漏之初显示的数据(即点的纵坐标)；

    (2)求反比例函数的表达式， 并确定车间内检测表恢复到气体泄漏之初数据时对应的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）

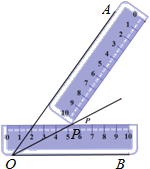
    A.角平分线上的点到这个角两边的距离相等

    B.角的内部到角的两边的距离相等的点在角的平分线上

    C.三角形三条角平分线的交点到三条边的距离相等

    D.以上均不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了更好改善河流的水质，治污公司决定购买10台污水处理设备现有A，B两种型号的设备，其中每台的价格，月处理污水量如下表：经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

    A型

    B型

    价格万元台

    a

    b

    处理污水量吨月

    240

    200

    求a，b的值；

    治污公司经预算购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案；

    在的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

    查看答案和解析>>

    同步练习册答案