
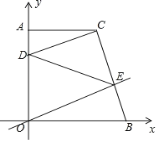
����Ŀ����ͼ��������y=x2��4x��5��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C�������ߵĶԳ�����x�ύ�ڵ�D��
��1����A��B��C��������꼰�����ߵĶԳ��ᣮ
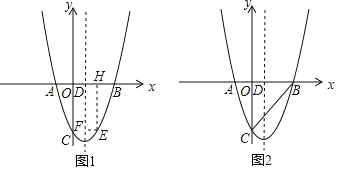
��2����ͼ1����E��m��n��Ϊ��������һ�㣬��2��m��5������E��EF��x�ᣬ�������ߵĶԳ����ڵ�F����EH��x���ڵ�H�����ı���EHDF�ܳ������ֵ��
��3����ͼ2����PΪ�����߶Գ�����һ�㣬�Ƿ���ڵ�P��ʹ�Ե�P��B��CΪ�������������ֱ�������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A����1��0����B��5��0����C��0����5����x=2����2��![]() ����3�����ڣ���P������Ϊ��2��3����2����7����2����6����2��1����
����3�����ڣ���P������Ϊ��2��3����2����7����2����6����2��1����
��������
��1���ֱ���x=0��y=0���������ߵĽ���ʽ�У��ɵ�A��B��C�����꣬���ݶԳ�
�ԣ��ɵöԳ��
��2�����ݾ����ܳ���ʽ��ʾ�ı���EHDF�ܳ��������ݶ��κ����Ķ���ʽ�ɵ��ı���EHDF
�ܳ������ֵ��
��3�������������
�ٵ���CBP=90��ʱ����ͼ2��������PDB�ס�BOC���б���ʽ�ã�PD=DB���ɵý��ۣ�
�ڵ���BCP=90��ʱ����ͼ3��������PCG�ס�BDG����![]() =
=![]() ���ɵ�PG�ij����Ӷ�д��P
���ɵ�PG�ij����Ӷ�д��P
�����ꣻ
����ABΪֱ����Բ�����Գ�����P1��P2����ͼ4��������P1DB�ס�CHP1����![]() ��
��
�з��̿ɵý��ۣ�
�⣺��1����x=0ʱ��y=��5��
��C��0����5����
��y=0ʱ��x2��4x��5=0��
x1=5��x2=��1��
��A����1��0����B��5��0����
�ɶԳ��Եã������ߵĶԳ����ǣ�![]()
��2����ͼ1����E��m��n������2��m��5��
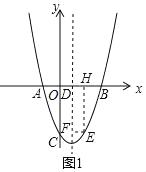
��E�ڵ������ޣ�
��EF=m��2��EH=n=��m2+4m+5��
���ı���EHDF�ܳ�ΪW��
��W=2��EF+EH��=2��m��2��m2+4m+5��=��2m2+10m+6![]()
�ߩ�2��0��
�൱![]() ʱ���ı���EHDF�ܳ������ֵ��
ʱ���ı���EHDF�ܳ������ֵ��![]() ��
��
��3����P��2��y����
�����������
�ٵ���CBP=90��ʱ����ͼ2��
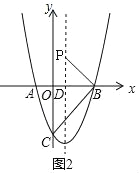
���PBO=��OCB��
�ߡ�PDB=��COB=90����
���PDB�ס�BOC��
��![]()
��PD=DB��
��y=5��2=3��
��P��2��3����
�ڵ���BCP=90��ʱ����ͼ3��
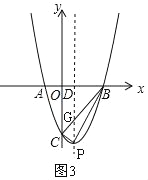
�ߡ�OBC=45����
���GDB�ǵ���ֱ�������Σ�
��BD=DG=3��
��![]()
��![]()
��![]()
�ߡ�PCG�ס�BDG��
��![]()
��![]()
��PG=4��
��P��2����7����
����ABΪֱ����Բ�����Գ�����P1��P2����ͼ4�����CP1B=��CP2B=90����
��C��CH�ͶԳ�����H��
���P1DB�ס�CHP1��
��![]() ,
,
��![]()
��y1=��6���ᣩ��y2=1��
��P1��2��1����
ͬ���ã�P2��2����6����
������������P��������2��3����2����7����2����6����2��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ������У�������ƻ����������ͻ������������繲200�ã���ͨ�������˽��������15�ù�����6�û���������600Ԫ��������12�ù�����5�û���������490Ԫ��
��1�����Ĺ����ͻ������ĵ��۸��Ƕ���Ԫ��
��2����֪�ס����������Ե������������ۼ۸�������۸�һ�������������Żݣ������ԣ�ÿ����һ�û����������ù��������������������9�ۣ������ԣ�����Ļ�������������7�ۣ��蹺�������x�ã�y1��y2�ֱ��ʾ���ס������������й������������ܷ��ã����y1��y2����x�ĺ�������ʽ��
��3�����ڣ�ѧУ����ʵ����Ҫ����Ļ������Ŀ���������35���Ҳ�����40�ã������һ�ֹ�����ʹ��������������ѵ��ܷ������٣����ٷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ���ż��ڼ䣬С����С�����������Ĵ���������ΪA������¹ԭ����ΪB�������칫����ΪC�����������ֲ������ΪD���е�һ������ȥ���棬���Ǹ��������ĸ���������ѡһ����ÿ�����㱻ѡ�еĿ�������ͬ
��1����С��ѡ��ȥ��¹ԭ����ĸ��ʣ�
��2������״ͼ���б��ķ�����С����С��ѡ��ȥͬһ���ط�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5�ű��濴��ȥ�����˿��ƣ�����ֱ�д��5��6��7��8��9��ϴ�Ⱥ��������·��������ϣ����������ȡ2�ţ�����Ŀ�Ƭ�ϵ�����ǡ�����������������ĸ�����__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������֯������ʵʮ�Ŵ��������λ���ж�����ʦ�ݽ����������ݸ�У�����ɼ���Сѧ�顢��ѧ��ֱ�ѡ��10����ʦ�μӾ�������Щѡ�ֵľ����ɼ���ͼ��ʾ��
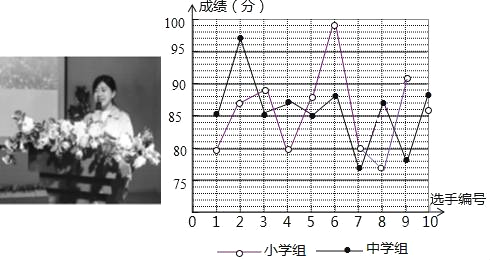
������ͼ�ṩ����Ϣ���ش��������⣺
��1���������������������
����ɼ� | ���� | ƽ���� | ���� |
Сѧ�� | ���� | 85.7 | 39.6 |
��ѧ�� | 85 | ���� | 27.8 |
��2������ƽ�����뷽�����Ϊ�ĸ��������ɼ�����Щ����˵�����ɣ�
��3������ÿ��ľ���ѡ���зֱ�ѡ��3�˲μ��ܾ���������Ϊ�ĸ����ʤ�Ŀ����Դ�Щ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��D����ABC�ı�AB�ϣ���AD��CD��

��1����ֱ�ߺ�Բ������BDC��ƽ����DE����BC�ڵ�E����д������������ͼ�ۼ�����
��2���ڣ�1���������£��ж�DE��AC��λ�ù�ϵ����д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��BC����һ���㣬��E��F�ֱ���AB��AC���ϣ�����AD��DE��DF���ҡ�ADE=��ADF=60�㣮
С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У�ʼ����AE=AF��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������AD�ǡ�EDF�Ľ�ƽ���ߣ������ADF��ȫ�������Σ�Ȼ��ͨ�����������ε����֪ʶ��֤��
�뷨2������AD�ǡ�EDF�Ľ�ƽ���ߣ������ƽ���ߵ����ʶ����Ļ���ͼ�Σ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
�뷨3������ACD�Ƶ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
����ο�������뷨������С��֤��AE=AF����һ�ַ������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ������Ϊ��3��4����
������Ϊ��3��4����![]() ���ڵ�
���ڵ�![]() ��
��![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() ��ԭ��
��ԭ��![]() ��������
��������![]() ���������˶���
���������˶���![]() ��ֱ��
��ֱ��![]() ����
����![]() ����
����![]() ������� ��
������� ��
A.���B.�ȱ����СC.��СD.ʼ�ղ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫ���һ���������εĻ�̳����̳�ϵ�![]() �ף��µ�
�ף��µ�![]() �ף����µ����
�ף����µ����![]() �ף��������е����ߣ����ߣ�����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊ
�ף��������е����ߣ����ߣ�����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊ![]() �ף�
�ף�
![]() �ú�
�ú�![]() ��ʽ�ӱ�ʾ�������������
��ʽ�ӱ�ʾ�������������
![]() �����������������������İ˷�֮һʱ�������Ŀ���
�����������������������İ˷�֮һʱ�������Ŀ���
![]() ������Ƶ�Ҫ�����Ŀ����ܳ���
������Ƶ�Ҫ�����Ŀ����ܳ���![]() �ף�����������ܷ��ã���Ԫ�������Ŀ��ȳ���������ϵ������ϵ����
�ף�����������ܷ��ã���Ԫ�������Ŀ��ȳ���������ϵ������ϵ����![]() ����̳���ಿ�ֵ��̻�����Ϊÿƽ����
����̳���ಿ�ֵ��̻�����Ϊÿƽ����![]() ��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ������٣����ٷ����Ƕ�����Ԫ��
��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ������٣����ٷ����Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com