
����Ŀ����ͼ��Ҫ���һ���������εĻ�̳����̳�ϵ�![]() �ף��µ�
�ף��µ�![]() �ף����µ����
�ף����µ����![]() �ף��������е����ߣ����ߣ�����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊ
�ף��������е����ߣ����ߣ�����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊ![]() �ף�
�ף�
![]() �ú�
�ú�![]() ��ʽ�ӱ�ʾ�������������
��ʽ�ӱ�ʾ�������������
![]() �����������������������İ˷�֮һʱ�������Ŀ���
�����������������������İ˷�֮һʱ�������Ŀ���
![]() ������Ƶ�Ҫ�����Ŀ����ܳ���
������Ƶ�Ҫ�����Ŀ����ܳ���![]() �ף�����������ܷ��ã���Ԫ�������Ŀ��ȳ���������ϵ������ϵ����
�ף�����������ܷ��ã���Ԫ�������Ŀ��ȳ���������ϵ������ϵ����![]() ����̳���ಿ�ֵ��̻�����Ϊÿƽ����
����̳���ಿ�ֵ��̻�����Ϊÿƽ����![]() ��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ������٣����ٷ����Ƕ�����Ԫ��
��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ������٣����ٷ����Ƕ�����Ԫ��
���𰸡�![]() �����������Ϊ��
�������������![]() ��
��![]() ���Ŀ�Ϊ
���Ŀ�Ϊ![]() �ף�
�ף�![]() ���ٷ���Ϊ
���ٷ���Ϊ![]() ��Ԫ��
��Ԫ��
��������
��1������������״�����Σ����Ը������������ʽ������⣻
��2���ú�x�Ĵ���ʽ��ʾ�����������������Ȼ��������ε����������������ͨ�����������������İ˷�֮һ�з�����⣬����������Ҫע�����������غϲ��֣�
��3����ʾ������̳���ܷ��������Ŀ���֮��ĺ�����ϵʽ��ת���ɺ�������ֵ���������⼴�ɣ�
![]() �������������
�������������![]() ��
��
![]() �������������
�������������![]() ��
��
�������Ϊ![]() ��
��
�����⣺![]() ��
��
�����ã�![]() ��
��
![]() ��
��![]() �����������⣬��ȥ����
�����������⣬��ȥ����
�����Ŀ�Ϊ![]() �ף�
�ף�
![]() ��̳�ϵ�
��̳�ϵ�![]() �ף��µ�
�ף��µ�![]() �ף����µ����
�ף����µ����![]() �ף�
�ף�
�������������![]() ��
��
���������Ϊ![]() ��
��
�̻������Ϊ![]() ��
��
��̳�ܷ���![]() ���ܷ���+�̻��ܷ��ã�
���ܷ���+�̻��ܷ��ã�
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() ��ֵ��С��
��ֵ��С��
�߸�����Ƶ�Ҫ�����Ŀ����ܳ���![]() �ף�
�ף�
�൱![]() ��ʱ���ܷ������٣�
��ʱ���ܷ������٣�
�����ٷ���Ϊ��![]() ��Ԫ��
��Ԫ��


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
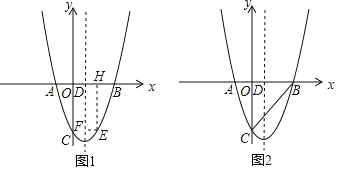
����Ŀ����ͼ��������y=x2��4x��5��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C�������ߵĶԳ�����x�ύ�ڵ�D��
��1����A��B��C��������꼰�����ߵĶԳ��ᣮ
��2����ͼ1����E��m��n��Ϊ��������һ�㣬��2��m��5������E��EF��x�ᣬ�������ߵĶԳ����ڵ�F����EH��x���ڵ�H�����ı���EHDF�ܳ������ֵ��
��3����ͼ2����PΪ�����߶Գ�����һ�㣬�Ƿ���ڵ�P��ʹ�Ե�P��B��CΪ�������������ֱ�������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ24�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60��õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ�ǣ�������

A. 12B. 6C. 3D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ũҵ��������ָ���£�С���ҽ�����ֲ��⨺���ϲ����գ�ȥ��⨺��ҵ��������12000Ԫ������⨺��ҵ������ȥ��������20%��֧������10%���������Ԥ�Ʊ�ȥ���11400Ԫ������㣺
��1��������� Ԫ��
��2������ȥ�������Ϊ![]() Ԫ��֧��Ϊ
Ԫ��֧��Ϊ![]() Ԫ������������Ϊ Ԫ��֧��Ϊ Ԫ�����������ú�
Ԫ������������Ϊ Ԫ��֧��Ϊ Ԫ�����������ú�![]() ��
��![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��3���з��������С���ҽ�����ֲ⨺��ҵ������֧����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
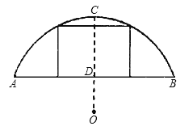
����Ŀ����ͼ��ʾ��ij����һ��Բ���εĹ��ţ�����ˮ���Ϊ8�ף���AB=8�ף��������߳�ˮ��Ϊ2�ף���CD=2�ף���
��1����������������Բ�İ뾶��
��2������һ�ҿ�6�ף����ն���Ϊ�����β��߳�ˮ��1.5�Ļ���Ҫ���������ʱ������˳��ͨ��������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ����������з��̣�
(1)x2+4x+4=9
(2)3x��2x+1��=4x+2��
(3)3��x��1��2=x��x��1��
(4)3x2��6x��2=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����DΪ
����DΪ![]() ���е㣬ֱ��
���е㣬ֱ��![]() �Ƶ�D��ת��
�Ƶ�D��ת��![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ����E��F���㣬���н��ۣ���
����E��F���㣬���н��ۣ���![]() �ǵ���ֱ�������Σ���
�ǵ���ֱ�������Σ���![]() ����
����![]() ����
����![]() ��������ȷ������( ).
��������ȷ������( ).

A.�٢ڢ�B.�ڢۢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����2m+1��x+m��m+1��=0��
��1����֤������������������ȵ�ʵ������
��2���跽�̵������ֱ�Ϊx1��x2����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
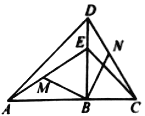
����Ŀ����ͼ��![]() �У�
�У�![]() �Ǹߣ���
�Ǹߣ���![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ��
��
��1����֤��![]() ��
��
��2��̽��![]() ��
��![]() �Ĺ�ϵ����֤����Ľ��ۣ�
�Ĺ�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com