
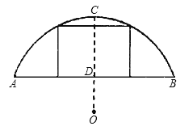
【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽为8米(即AB=8米),拱顶高出水面为2米(即CD=2米).
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽6米,船舱顶部为正方形并高出水面1.5米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
【答案】(1)r=5;(2)货船不可以顺利通过这座拱桥.
【解析】
(1)连接OA,设这座拱桥所在圆的半径为r米,由垂径定理可得AD=![]() AB=4,在Rt△AOD中,根据勾股定理得方程r2=42+(r-2)2,解此方程即可求得答案;(2)连接OM,设MN=5,根据勾股定理求得OH的长,即可求得HD的长,与1.5米比较,即可得到此时货船能否顺利通过这座拱桥.
AB=4,在Rt△AOD中,根据勾股定理得方程r2=42+(r-2)2,解此方程即可求得答案;(2)连接OM,设MN=5,根据勾股定理求得OH的长,即可求得HD的长,与1.5米比较,即可得到此时货船能否顺利通过这座拱桥.
(1)连接OA ,
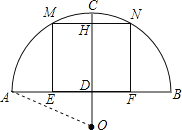
设OA=r,则OD=OC-CD=r-2,AD=![]() AB=4,
AB=4,
在Rt△AOD中,∵OA2=AD2+OD2,
∴r2=42+(r-2)2
∴r=5 .
(2)货船不能顺利通过这座拱桥.理由:
连接OM,由题意可知MN=6米,
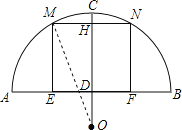
∵OC⊥MN,
∴MH=![]() MN=3米,
MN=3米,
在Rt△OMH中,OH=![]() =4米,
=4米,
∵OD=OC-CD=5-2=3米
∵DH=OH-OD=4-3=1米<1.5米,
∴货船不能顺利通过这座拱桥.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】某教育局组织了“落实十九大精神,立足岗位见行动”教师演讲比赛,根据各校初赛成绩在小学组、中学组分别选出10名教师参加决赛,这些选手的决赛成绩如图所示:
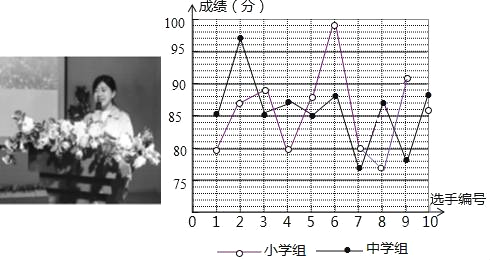
根据上图提供的信息,回答下列问题:
(1)请你把下面表格填写完整:
团体成绩 | 众数 | 平均数 | 方差 |
小学组 |
| 85.7 | 39.6 |
中学组 | 85 |
| 27.8 |
(2)考虑平均数与方差,你认为哪个组的团体成绩更好些,并说明理由;
(3)若在每组的决赛选手中分别选出3人参加总决赛,你认为哪个组获胜的可能性大些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
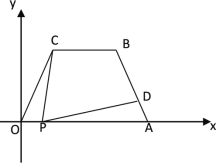
【题目】如图所示,在平面直角坐标中,四边形OABC是梯形,且AB = OC = 4,CB∥OA,OA = 7,∠COA = 60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D,
(1)求点B的坐标;
(2)当点P运动什么位置时,使得∠CPD =∠OAB,且![]() ,求这时点P的坐标;
,求这时点P的坐标;
(3)当点P运动什么位置时,△OCP为等腰三角形,直接写出这时点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
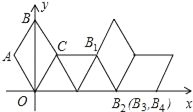
【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
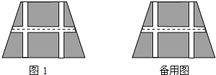
【题目】如图,要设计一个等腰梯形的花坛,花坛上底![]() 米,下底
米,下底![]() 米,上下底相距
米,上下底相距![]() 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为![]() 米.
米.
![]() 用含
用含![]() 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
![]() 当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
![]() 根据设计的要求,甬道的宽不能超过
根据设计的要求,甬道的宽不能超过![]() 米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是
米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是![]() ,花坛其余部分的绿化费用为每平方米
,花坛其余部分的绿化费用为每平方米![]() 万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 在同一条直线上,连结
在同一条直线上,连结![]() .
.
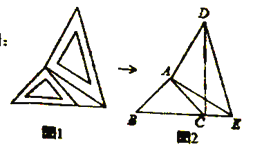
(1)请在图2中找出与![]() 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),在
重合),在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和等边三角形
和等边三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,以下结论一定正确的有( )个
,以下结论一定正确的有( )个
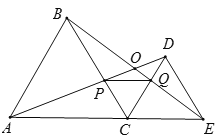
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]()
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
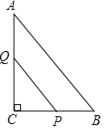
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在边BC、AC上,PQ∥AB,把△PCQ绕点P旋转得到△PDE(点C、Q分别与点D、E对应),点D落在线段PQ上,若AD平分∠BAC,则CP的长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com